IX. Дисперсионный анализ

Из анализа общих интенсивных показателей такой вывод сделать нельзя, так как на общие показатели оказал влияние разный состав осмотренных по полу в этих районах. Из литературных данных известно, что стенокардия приблизительно в 2 раза чаще встречается среди мужчин, чем среди женщин. Поэтому в 1-ом районе, где были обследованы преимущественно мужчины, общий интенсивный показатель был завышен (4,2 на 100 обследованных), а во 2-ом районе – занижен (3,8 на 100 обследованных), так как были обследованы в основном женщины. Метод стандартизации позволил увидеть истинную картину заболеваемости, устранив влияние фактора, связанного с полом обследованных.

ЗАДАНИЯ

Запустите программу Excel, откройте файл в папке своей учебной группы под именем «Статистика–Фамилии студентов». На листе «Стандартизация», решите требуемый вариант заданий, сохраните изменения и покажите результат работы преподавателю.

Вариант 1

Проведено изучение заболеваемости населения в городах N и M. В городе N проживало 30000 человек, из них 20000 мужчин и 10000 женщин. В течение года болели 5000 мужчин и 4000 женщин. В городе М проживало 65000 человек (25000 мужчин, 40000 женщин). Болели в течение года 7000 мужчин и 14000 женщин. Рассчитать интенсивные и стандартизованные показатели заболеваемости (на 1000 жителей), проанализировать и оценить достоверность различий между ними, сделать вывод.

Вариант 2

Требуется сравнить физическое развитие учеников 8-10 классов в 2-х школах. В 1-й школе обследовано 195 человек, из них 31 мальчик и 164 девочки, выявлено, что отставание физического развития есть у 1-го мальчика и 5-ти девочек.

Во 2-й школе обследовано 182 человека, из них 125 мальчиков и 57 девочек, имели отставание 5 мальчиков и 4 девочки. Рассчитать интенсивные и стандартизованные показатели частоты отклонений физического развития детей в этих школах, сравнить их и оценить достоверность различий между ними, сделать вывод.

Вариант 3

Необходимо сравнить качество протезирования зубов в 2-х стоматологических поликлиниках. В 1-й поликлинике изготовлено 400 протезов, из них 35 мостовидных и 365 единичных; плохая фиксация протезов зафиксирована у 1-го пациента с мостовидным и 5-ти пациентов с единичными протезами. Во 2-й поликлинике установлено 350 протезов, из них 250 мостовидных и 100 единичных; нарушение фиксации обнаружено 5-и пациентов с мостовидными и 4-х с единичными протезами. Рассчитать интенсивные и стандартизованные показатели качества протезирования в поликлиниках, проанализировать и оценить достоверность различий между ними, сделать вывод.

Вариант 4

Сравните загрязненность воздуха по количеству проб, не отвечающих санитарным требованиям, в 2-х районах города N. В 1-м районе взято 300 проб, из них 30 в жилых кварталах и 270 вблизи автомобильных дорог; обнаружено несоответствие требованиям в 2-х квартальных пробах и 5 у автодороги. Во 2-м районе взято 200 проб, из них 150 квартальных и 50 у дороги; имели отклонение от норматива загрязненности 5 квартальных и 4 пробы рядом с автодорогой. Рассчитать интенсивные и стандартизованные показатели загрязненности воздуха в 2-х районах, проанализировать и оценить достоверность различий между ними, сделать вывод.

Вариант 5

Требуется сравнить качество работы 2-х лечебно-профилактических учреждений (ЛПУ) по числу послеоперационных осложнений. В 1-й клинике проведено 600 хирургических операций, из них 55 полостных в общем отделении и 545 малоинвазивных в эндоскопическом отделении; послеоперационные осложнения зафиксированы у 20-и пациентов, перенесших полостную операцию, и у 5-ти пациентов из эндоскопического отделения. Во 2-й клинике выполнено 350 операций, из них 250 полостных и 100 малоинвазивных; осложнения были зафиксированы у 5-и пациентов общего отделения и у 4-х - эндоскопического. Рассчитать интенсивные и стандартизованные показатели послеоперационных осложнений в 2-х ЛПУ, проанализировать и оценить достоверность различий между ними, сделать вывод.

Вариант 6

Сравните загрязненность 2-х водоемов по количеству проб, не отвечающих санитарным требованиям. В 1-м водоеме взято 300 проб, из них 30 поверхностных и 270 с глубины 3 метра; обнаружено несоответствие требованиям в 5-ти поверхностных пробах и 7-ми глубинных. Во 2-м водоеме взято 200 проб, из них 150 поверхностных и 50 глубинных; имели отклонение от норматива загрязненности 8 поверхностных и 3 глубинные пробы. Рассчитать интенсивные и стандартизованные показатели загрязненности водоемов, проанализировать и оценить достоверность различий между ними, сделать вывод.

Контрольные вопросы

1. В каких случаях применяется метод стандартизации?

2. В чем заключается суть метода стандартизации?

3. Назовите модификации метода стандартизации?

4. Назовите этапы прямого метода стандартизации.

5. О чем свидетельствуют стандартизованные показатели?

Рекомендуемая литература:

1. Информатика. Книга 2. Основы медицинской информатики: учебник / В.И. Чернов, И. Э. Есауленко, М В. Фролов и др. – М.: Дрофа, 2009. – 205, [3] с.: ил.

2. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения [Электронный ресурс]: учебное пособие для практических занятий / под ред. В.З. Кучеренко. - 4-е изд., перераб. и доп. - М.: ГЭОТАР-Медиа, 2011. - 256 с. – Режим доступа: http://www.studmedlib.ru

Трудно представить любое медицинское исследование (социально-гигиеническое, гигиеническое, клиническое, экспериментальное и др.), в котором не ставилась бы в той или иной мере задача определения силы влияния различных факторов на размеры изучаемого признака. Определяя различия средних арифметических двух выборочных групп наблюдения путем расчета критерия Стьюдента t, который позволяет выявить статистическую значимость разницы средних, исследователь подразумевает, как само собой разумеющееся, что группы исследуемых совершенно однородны и отличаются только по одному какому-то признаку или методу воздействия на них.

Между тем на практике это условие соблюдается далеко не всегда. На изучаемое явление и, следовательно, его средний уровень оказывают влияние многочисленные факторы, как постоянные (планируемые или сознательно выделяемые для их изучения), так и случайные (неопределенные). Например, больные гипертонической болезнью, отобранные по полу, возрасту, стадии и длительности заболевания, помимо болезни, подвергаются воздействию других неучтенных факторов, в результате чего у разных больных наблюдается различный уровень артериального давления.

При изучении явлений, сравнении их друг с другом в поисках сходства и различий необходимо обращать внимание не только на величину средних, но и на разнообразие вариант, а также вариабельность изучаемых признаков. Исследователь может встретить вариационные ряды, не отличающиеся по центральной тенденции (размеру средней арифметической), но различные по степени варьирования. И наоборот - ряды, одинаковые по величине разброса вариант, могут различаться по размерам средней арифметической. Установление значимости различий средних арифметических, измерение степени влияния факторов и их градаций на варьирующий (результативный) признак наиболее эффективно достигаются путем применения дисперсионного анализа. Впервые основа дисперсионного анализа была разработана известным английским статистиком Р. Фишером в 1925 году.

Дисперсионный анализ – это метод в статистической математике, направленный на поиск зависимостей в экспериментальных данных путём исследования значимости различий вариабельности признака в исследуемой совокупности. В литературе также встречается обозначение ANOVA (от англ. ANalysis Of VAriance). Он базируется на определении степени рассеяния (дисперсии) оцениваемых признаков в нескольких группах. Это позволяет измерить силу влияния отдельных факторов на значения показателей.

Известно, что величина отдельных признаков представляет собой результат воздействия разнообразных факторов, различных по силе влияния. Одни факторы имеют значительно большую силу влияния, другие - меньшую. Причем, как правило, факторы сами воздействуют друг на друга, сочетая свое влияние, иногда усиливают действие друг друга, иногда, наоборот, погашают это действие. Преимуществом дисперсионного анализа является то, что он дает возможность изучить и сравнить роль каждого из них.

В отличие от дисперсионного анализа другие общепринятые в медицинских исследованиях статистические методы обработки, как правило, предусматривают проведение попарных сравнений, что приводит к огромному объему расчетов и часто не дает полной оценки.

Сущность дисперсионного анализа заключается в изучении статистического влияния одного или нескольких факторов на результативный признак.

Результативный признак - это элементарное свойство объектов, изучаемое как результат влияния факторов: организованных в исследовании (основных - х) и всех остальных, неорганизованных, не учтенных в данном исследовании (случайных - z).

Фактор - это влияние, воздействие или состояние, которое отражается на размерах и разнообразии результативного признака.

Градации фактора - это степень его воздействия (нулевое действие в контрольной группе) или состояние объектов изучения (пол, возраст и т.д.).

Дисперсионный комплекс - это совокупность градаций комплекса данных (опытных групп исследования) с привлеченными для исследования значениями и средними величинами по каждой градации.

Комплексы, составленные по принципу случайной выборки, называются рандомизированными.

При изучении количественных признаков в градации комплекса заносятся числовые результаты измерения изучаемого признака у каждого отдельного объекта. При изучении качественных признаков в градации комплекса заносится число объектов с наличием признака и общее число объектов.

Статистическое влияние - это отражение в разнообразии результативного признака того разнообразия фактора (его градаций), которое организовано в исследовании.

Сумма основных и случайных факторов составит общие факторы (у). Результативный признак изучается как результат воздействия факторов, организованных в исследовании (х) и неорганизованных (z).

Общее влияние как раз и определяет влияние всех организованных и неорганизованных (случайных) факторов, определивших такое развитие признака, которое наблюдалось в дисперсионном комплексе. Общее влияние служит базой для определения доли влияний - факториальных и случайных.

Факториальное влияние - это простое или комбинированное статистическое влияние изучаемых (учтенных) факторов.

Случайное влияние - это действие тех факторов, которые не учтены в дисперсионном комплексе и составляют общий фон, на котором действуют учитываемые факторы.

Таким образом, дисперсионный анализ исследует важнейшее свойство совокупности – разнообразие (вариабельность, дисперсию) признака. Для этого выделяется три вида разнообразия: межгрупповое, внутригрупповое и общее. Межгрупповое разнообразие зависит от влияния исследуемого фактора, по которому выделяется каждая группа. Иными словами, межгрупповое разнообразие - это различие средних в каждой группе. Внутригрупповое разнообразие зависит от силы влияния каких-то неучтенных случайных факторов. Общее разнообразие складывается из межгруппового и внутригруппового.

В основе дисперсионного анализа лежит предположение о том, что одни переменные могут рассматриваться как причины (факторы, независимые переменные): f₁, …, f_k, а другие как следствия (зависимые переменные). Независимые переменные называют иногда регулируемыми факторами именно потому, что в эксперименте исследователь имеет возможность варьировать ими и анализировать получающийся результат.

Основной целью дисперсионного анализа является исследование значимости различия между группами с помощью сравнения дисперсий. Разделение общей дисперсии на несколько источников позволяет сравнить дисперсию, вызванную различием между группами, с дисперсией, вызванной внутригрупповой изменчивостью. При истинности нулевой гипотезы (о равенстве средних в нескольких группах наблюдений, выбранных из генеральной совокупности), оценка дисперсии, связанной с внутригрупповой изменчивостью, должна быть близкой к оценке межгрупповой дисперсии. Если выполняется сравнение средних в двух выборках, дисперсионный анализ даст тот же результат, что и обычный t-критерий Стьюдента. Однако, помимо этого, он позволяет оценить степень такого влияния, а также может использоваться при сопоставлении более чем 2-х групп.

Сущность дисперсионного анализа заключается в расчленении общей дисперсии (D или SS) изучаемого признака на отдельные компо­ненты, обусловленные влиянием конкретных факторов, и проверке гипотез о значимости влияния этих факторов на исследуемый признак. Обозначе­ние SS - это сокращение от фразы "суммы квадратов" (Англ. sum of squares). Оно чаще всего используется в зарубежных источниках.

Сравнивая компоненты дисперсии друг с другом посредством F-критерия Фишера, можно определить, какая доля общей вариативности результативного признака обусловлена действием регулируемых факторов.

Критерий Фишера экспериментальных (эмпирических) данных (F _Эмп.) вычисляется как отношение среднего квадрата дисперсии, обусловленной изучаемым фактором, к среднему квадрату случайной дисперсии:

,

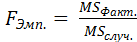где: F _Эмп. – критерий Фишера, вычисленный в исследуемой совокупности,

MS _Факт. – средний квадрат дисперсии, обусловленной изучаемым фактором,

MS _Случ. – средний квадрат дисперсии, обусловленной случайными факторами.

Для оценки достоверности полученного результата вычисленный на экспериментальных данных критерий Фишера сравнивают с его критическим значением (F _Крит.) для принятого уровня вероятности (p) и степеней свободы (df).

С целью уменьшения объема вычислений в программе Excel может применяться надстройка «Анализ данных» и ее модуль «Однофакторный дисперсионный анализ».

Дата добавления: 2014-12-23