Статистическая обработка экспериментальных данных

При проведении экспериментальных исследований важное значение имеет правильная математическая обработка полученных данных. Для определения некоторого показателя обычно проводят ряд параллельных опытов, в результате получают несколько различных значений этого показателя. Возникает вопрос об истинном значении исследуемой величины, ее точности и достоверности.

Математическая оценка достоверности количественных показателей, полученных в процессе научного эксперимента, является одновременно оценкой надежности выводов и практических предложений.

Результаты зависят от множества причин и редко повторяются, следовательно, что бы получить более полное представление о наблюдаемом явлении, надо знать несколько результатов, не менее трех.

За истинное значение обычно принимают, среднее арифметическое, полученных данных, затем определяют меру рассеивания полученных значений вокруг среднего и оценивают точность и достоверность полученного результата. Рассмотрим подробнее порядок проведения математической обработки результатов эксперимента.

Пусть требуется изучить совокупность однородных объектов относительно некоторого количественного признака.

Таким признаком может быть в партии изделий, отобранных для контроля: вес изделия, содержание в нем некоторых веществ, прочность изделия и т.д.

Иногда проводят сплошное обследование, но чаще – выборочное.

Выборочной совокупностью, или просто выборкой, называют совокупность случайно отобранных объектов.

Генеральной называют всю совокупность объектов.

Существует несколько методов отбора. Мы будем рассматривать собственно случайную повторную выборку – отдельные элементы отбираются случайным образом, причем обследованный элемент возвращается в совокупность.

Судить по данным выборки об интересующем нас признаке генеральной совокупности с достаточной степенью уверенности можно лишь в том случае, когда объекты выборки правильно представляют совокупность. Данное требование формулируется так: выборка должна быть репрезентативной (представительной).

Рассмотрим некоторую совокупность для изучения количественного признака Х. Наблюдаемые значения х_i признака Х называются вариантами, а последовательность вариант в возрастающем порядке - вариационным рядом.

Статистическим распределением называют перечень вариант х_i и соответствующим им частот п _i (сумма всех частот равна объему выборки п).

Рассмотрим числовые характеристики статистического распределения: среднюю арифметическую (), дисперсию (D) и среднее квадратическое отклонение (s):

.

D – средняя арифметическая квадратов отклонения вариант от их средней. Она характеризует рассеивание (разброс) вариант относительно .

Если эти характеристики вычислены для генеральной совокупности, то они называются генеральными и обозначаются: , D_в, s_в.

Ошибкой репрезентативности (достоверности) называется расхождение характеристик признака в генеральной и выборочной совокупностях, возникающее в результате того, что исследуется не вся совокупность, а лишь ее часть.

Математическая теория выборочного метода состоит в определении средней величины случайных ошибок репрезентативности и их возможных границ.

В математической статистике доказано, что выборочная средняя является несмещенной оценкой генеральной средней, т. е. ее математическое ожидание равно :

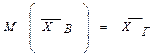
Выборочная же дисперсия не является несмещенной оценкой генеральной дисперсии:

Поэтому для оценки генеральной дисперсии вводят так называемую «исправленную» дисперсию выборки и, соответственно, «исправленное» среднее квадратическое отклонение s.

Эта оценка уже является несмещенной.

Итак, для оценки генеральной средней мы имеем и s - исправленное среднее квадратическое отклонение выборки.

Вероятность того, что абсолютная величина отклонения выборочной средней от генеральной не превзойдет некоторого постоянного числа Δ, называется доверительной вероятностью (γ), или надежностью, а интервал ( - Δ; - Δ) - доверительным интервалом.

Выборочная средняя является случайной величиной, распределенной по нормальному закону. Поэтому доверительная вероятность определяется по формуле:

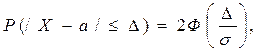(16)

где Х – выборочная средняя, а ее математическое ожидание равно генеральной средней;

– среднее квадратическое отклонение.

Ф(t) – функция Лапласа.

Ф(t) 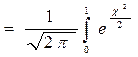dx,

ее значения представлены в таблице [23]

где называют средней квадратической ошибкой и обозначают m:

m = ,

где S – исправленное среднее квадратическое отношение;

n – объем выборки.

Из (16) по заданной доверительной вероятности можно определить значение D:

По таблице значений Ф(t) находим значение аргумента t, соответствующее Ф(t)=g/2. Он обозначается t_g и называется коэффициентом доверия.

Отсюда D = t_g ·m - предельная ошибка выборки с доверительной вероятностью g.

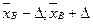() – доверительный интервал с той же вероятностью.

Обычно применяют значения коэффициента: t_g = 2 при g = 0,954; t_g = 3 при g = 0,997.

При малых выборках t_g определяется: t_g= t(g, n) (таблица 15).

Запишем теперь основные этапы статистического исследования по данной выборке объема n.

1. Находим среднюю арифметическую (взвешенную):

2. Находим «исправленное» среднее квадратическое отклонение S:

При больших n можно использовать среднее квадратическое отклонение:

3. Определяем коэффициент вариации:

4. Определяем среднюю квадратическую ошибку выборки по формуле:

5. Находим предельную ошибку выборки с заданной достоверной вероятностью γ:

,

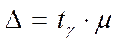где t_γ определяется по таблице Лапласа, как указано выше, или по таблице 15 для малой выборки (n< 30), t_γ = t (γ,n).

6. Находим доверительный интервал, в котором находится искомая генеральная средняя с заданным уровнем надежности γ:

()

Таблица 15 – Таблица значений t_γ = t (γ,n)

γ n	0,95	0,99	0,999	γ n	0,95	0,99	0,999
	2,78	4,60	8,61		2,093	2,861	3,883
	2,57	4,03	6,86		2,064	2,797	3,745

Продолжение таблицы 15

	2,45	3,71	5,96		2,045	2,756	3,659
	2,37	3,50	5,41		2,032	2,729	3,600
	2,31	3,36	5,04		2,023	2,708	3,558
	2,26	3,25	4,78		2,016	2,692	3,527
	2,23	3,17	4,59		2,009	2,679	3,502
	2,20	3,11	4,44		2,001	2,662	3,464
	2,18	3,06	4,32		1,996	2,649	3,439
	2,16	3,01	4,22		1,001	2,640	3,418
	2,15	2,98	4,14		1,987	2,633	3,403
	2,13	2,95	4,07		1,984	2,627	3,392
	2,12	2,92	4,02		1,980	2,617	3,374
	2,11	2,90	3,97	∞	1,960	2,576	3,291
	2,10	2,88	3,92

Пример 1 с большой выборкой (n>30): Имеются данные обследования 50 семей с одинаковым уровнем дохода потребления рыбопродуктов на человека в кг (первые два столбца таблицы 16). Провести статистическую обработку данных.

Таблица 16 – Статистическая обработка данных потребления рыбопродуктов

Потребление рыбопродуктов на человека, кг, хi	Количество семей, ni	nixi
			- 2
			- 1
Итого

Заполним 3 – 6 столбцы рабочей таблицы и найдем:

σ = 1,22 s = 1,23

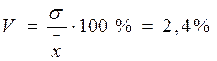
Найдем предельную ошибку и доверительный интервал с доверительной вероятностью γ = 0,954, то есть при t = 2:

Доверительный интервал:

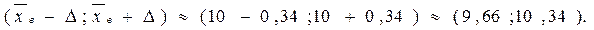
Итак, с надежностью 0,954 искомое среднее потребление рыбопродуктов находится в интервале 9,66≤ ≤ 10,34.

Пример 2 с малой выработкой (n<30).

Получены данные о содержании пектиновых веществ в пробах черники (столбец 1). Провести статистическую обработку данных.

Составим таблицу для вычислений.

Таблица 17 – Статистическая обработка данных пектиновых веществ в пробах черники

Содержание пектиновых веществ в чернике, хi %
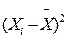
0,78	- 0,08	0,0064

Продолжение таблицы 17

0,78	- 0,08	0,0064
0,79	- 0,07	0,0049
0,89	0,03	0,0009
0,94	0,08	0,0064
0,99	0,13	0,169
Σ = 5,17		0,049

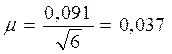
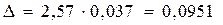
Доверительный интервал:

(0,86 – 0,0951; 0,86 + 0,0951) ≈ (0,7650;0,9551)

Среднее значение пектиновых веществ в чернике с вероятностью 0,95 находится в интервале 0,7650 = = 0,9551.

Примечание: Если экспериментальные данные получены с различной степенью точности, то результаты вычислений должны содержать столько значащих цифр после запятой, сколько их содержит наименее точное число [8,23].

Контрольные вопросы

1) Для чего используется математическое моделирование и комплексная оценка пищевых продуктов?

2) Укажите новые подходы и требования к разработке рецептур пищевых продуктов.

3) Какова методика математического расчета рецептуры пищевого продукта с заданным химическим составом?

4) Что включает в себя понятие и комплексная оценка комбинированного продукта с заданным химическим составом?

5) Для чего нужна статистическая обработка экспериментальных данных?

6) Что включает в себя понятие «выборка», «вариационный ряд», «ошибка репрезентативности», «доверительный интервал»?

7) Как рассчитываются:

- средняя арифметическая;

- дисперсия;

- среднее квадратичное отклонение;

- доверительная вероятность.

8) Дайте определение функции Лапласа.

9) Как находится «доверительный интервал»?

10) Как оформляется таблица «статистической обработки данных»?

Глава 3 Оформление дипломной работы

К оформлению работы дипломник приступает, когда основная часть экспериментальных исследований выполнена, сформулированы выводы и предложения, тщательно продуманы доказательства и иллюстрации.

Дата добавления: 2014-12-26