Гармонические колебания. Скорость и ускорение гармонических колебаний. Энергия гармонических колебаний

Колебательный процесс – процесс, повторяющийся во времени (биение сердца, дыхание, кровоток, смена дня и ночи, времён года)

Асцеляторы – всё, что может совершать колебания (листок, пружинный маятник, е вокруг ядра, сердце)

Устойчивые состояние – все колебания, процессы, не меняющие частоту колебаний.

Устойчивые колебания – асцеляторы меняют частоту колебаний.

Гармонические колебания – колебания, совершающиеся по законам sin или cos.

1) Математический маятник. На него действуют силы (векторы): T (сила натяжения нити длиной l = 2п*корень(l/g)), F (квазиупругая сила = -kx), mg (сила притяжения)

2) Пружинный маятник. На него действуют Fупр = -kx

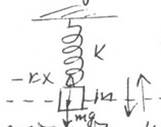
Уравнения, подчиняющие уравнения колебаний математического и пружинного маятника з-нам sin и cos:

x = Ao*sin(Wo*t+фи0)

x = Ao*cos(Wo*t+фи0)

x – мгновенное отклонение асцелятора от положения равновесия

Ao – const, максимальное отклонения асцелятора от положения равновесия

Wo – собственная частота асцелятора

фи0 – начальная фаза

Wo*t+фи0 – просто фаза

Часто гармонические колебания представляют в векторной форме или в виде вращения вектора. Для того, чтобы определить гармонические колебания в виде векторной формы, надо отложить модуль вектора, длину вектора, начальный угол с осью координат фи0, скорость вращения вектора W0

Скорость является первой производной от координаты по времени, величина численноа равная S, которое проходит тело за 1 ед. времени. V = x*1/t = A*W*cos(Wt+фи0) = Vo*cos(Wt+фи0) – уравнение скорости

Vo = W*A – амплитуда скорости

Ускорение – производная от скорости по времени: a = V*1/t = -A*W^2*sin(Wt+фи0) = a0*sin(Wt+фи0) – уравнение ускорения.

a0 = A*W^2 – амплитуда ускорения

Vo – в момент прохождения положения равновесия

Энергия гармонического колебания.

Рассмотрим колебания груза на пружине.

m – масса груза

k – коэффициент упругости пружины

Если пружину растянуть или сжать на величину x, то пружина запасается потенциальной энергией деформации:

Eп = k*x^2/2

x0 = A – амплитуда колебаний

т.к. x = x0*sin(Wt+фи0) – уравнение гармонических колебаний =>

Eп = 1/2k*A^2*sin^2(Wo*t+фи0) – уравнение потенциальной энергии в любой момент времени.

Кинетическая энергия определяется соотношением: Eк = m*Vmax^2/2, т.к. скорость – это производная координат по времени =>

V = x0*W*cos(Wo*t+фи0) – уравнение скорости. И тогда x0*W = Vmax – амплитуда скорости

Eк = 1/2m*A^2*Wo^2*cos^2(Wo*t+фи0)

m*Wo^2 = k, т.к. T = 2п*корень(m/k) – период колебаний. T = 2п/Wo = 1/Ню

Eк = 1/2k*A^2*cos^2(Wo*t+фи0) – уравнение кинетической энергии

Полная энергия колебаний E = Eк + Eп = 1/2k*A^2*sin^2(Wo*t+фи0) + 1/2k*A^2*cos^2(Wo*t+фи0) = 1/2k*A^2

E полная = 1/2k*x0^2

Дата добавления: 2014-12-26