Ряды предпочтительных чисел

Пределы метода.

Методы образования производных машин и их рядов на основе унификации не являются универсальными и всеобъемлющими. Каждый из них приложим к ограниченной категории машин. Многие машины (паровые и газовые турбины) по конструкции не допус­кают образования производных машин. Невозможно или нецелесообразно образовывать производные ряды для специализированных машин, машин большой мощности и т.д., которые остаются в категории индивиду­ального проектирования.

Унификация нередко сопровождается ухудшением качества, особенно в случае производных рядов большого диапазона. Крайние члены ряда по габаритам, металлоемкости, удельной массе и эксплуатационным пока­зателям, как правило, уступают специализированным машинам. Такое ухудшение можно допустить, если унификация обеспечивает большой экономический эффект, а габариты и масса имеют второстепенное значение.

Этот метод применим для машин общего назначения, ограниченно применим, а иногда и вовсе не применим для машин, к габаритам и массе которых предъявляют повышенные требования. В категории машины повышенного класса нередко приходится отказываться от уни­фикации и идти по пути индивидуального проектирования.

Основой нормализации являются ряды чисел, подчиняющихся определенным закономерностям. В арифметических рядах каждый член об­разуется прибавлением к предыдущему члену постоянного числа (разность прогрессии) τ.

Величина любого члена ряда а_к = а₀ +к _τ, где к — порядковый номер члена; а₀ - первый член ряда, которому присваивается нулевой номер.

Ниже показаны арифметические ряды с а₀ = 10, τ = 10 ¸ 1 в диапазоне к = 0 ¸ 30. При τ = 5 арифметический ряд в диапазоне наиболее употребительных в машиностроении диаметров В = 10 ¸ 100 мм следующий: 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70... 100.

Рис. Арифметические (а) и геометрические (б) ряды, к - порядковый номер члена ряда.

Арифметические ряды отличаются относительной неравномерностью. Их верхние области больше насыщены градациями размеров, а нижние меньше. Отношение каждого члена ряда к предыдущему имеет большую величину для первых членов ряда и резко уменьшается в верхних областях ряда.

Основные ряды. Стандарт устанавливает пять рядов предпочтительных чисел со знаменателем прогрессии , Степени n корня приняты равными 5, 10, 20, 40 и 80. Эти числа вместе с буквой R составляют обозначение ряда:

Ряды	R 5,	R 10	R 20	R 40	R 80
φ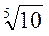

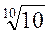
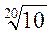
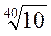
Величина любого члена ряда а_к = а₀ +кφ^к, где к - порядковый номер чле­на; а₀ — первый член ряда, которому присваивают нулевой номер.

С уменьшением φ интервалы между членами ряда уменьшаются, число членов ряда возрастает; ряд получается более дробным. Основные ряды предпочтительных чисел в диапазоне 1 ¸ 10

R5: 1; 1,6; 2,5; 4; 6,3; 10.

К10: 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10.

R40: 1; 1,06; 1,12; 1,18; 1,25; 32; 1,4; 1.5; 1,6; 1,7; 1,8; 1,9; 2; 2,12; 2,24; 2,36; 2,5; 2,65; 2.S; 3; 3,15; 3,35; 3,55; 3,75; 4; 4,25; 4,5; 4,75; 5; 5,3; 5,6; 6; 6.3; 6,7; 7,1; 7,5; 8; 8,5; 9; 9,5; 10.

Численные значения членов всех рядов округлены с погрешностью не более ±1%. Каждый более низкий ряд получается изъятием членов через один из ближайшего более высокого ряда.

Производные ряды. Из основных рядов можно получить геометри­ческие ряды для любого диапазона чисел, т. е. с любым значением начального и конечного членов. В соответствии с основным законом образования геометрических прогрессий производные ряды получают умножением первого члена нового ряда из числа любого их основных рядов (R5, К10 и. т. д.) вплоть до получения значения 10а, которое, в свою очередь, умножают на числа того же основного ряда и т. д.

Дата добавления: 2014-12-26