Следует иметь в виду, что при прочих одинаковых условиях жесткость равнопрочных деталей меньше, чем жесткость деталей, имеющих хотя бы местные повышенные запасы прочности

РАВНОПРОЧНОСТЬ

В случае кручения, изгиба и сложных напряженных состояний, когда равенство напряжений по сечению принципиально недостижимо, равно прочными считают детали, у которых одинаковые максимальные напряжения в каждом сечении (с учетом концентрации напряжений).

При изгибе условие равнопрочности заключается в одинаковости от­ношения рабочего изгибающего момента, действующего в каждом данном сечении, к моменту сопротивления данного сечения. При кручении это условие состоит в равенстве моментов сопротивления кручению каждого сечения детали, при сложных напряженных состояниях – в равенстве запасов надежности.

Понятие равнопрочности применимо и к нескольким деталям и к кон­струкции в целом. Равнопрочными являются конструкции, детали которых имеют одинаковый запас надежности по отношению к действующим на них нагрузкам. Это правило распространяется и на детали, выполненные из различных материалов: Так, равнопрочными являются стальная деталь с напряжением 200 МПа при пределе текучести σ_0,2 ~ 600 МПа и деталь из алюминиевого сплава с напряжением 100 МПа при σ_0,2 ~ 300 МПа. В обоих случаях коэффициент надежности равен 3. Это значит, что обе детали одновременно придут в состояние пластиче­ской деформации при повышении втрое действующих на них нагрузок. Независимо от этого каждая из сравниваемых деталей может еще обла­дать равнопрочностыо в указанном выше смысле, т. е. иметь одина­ковый уровень напряжений во всех сечениях.

Величину рабочих нагрузок и напряжений определяют расчетом. Деталь, рассчитанная как равнопрочная, будет действительно равнопрочной, если расчет правильно определяет истинные величины и распределение напря­жений во всех ее частях, что далеко не всегда имеет место.

Формы, требуемые условием равнопрочности, иногда трудно выпол­нить технологически и их приходится упрощать. Неизбежные почти во всякой детали дополнительные элементы (цапфы, буртики, канавки, выточки, резьбы), вызывающие иногда местное усиление, а чаще концентрацию на­пряжений и местное ослабление детали, также вносят поправки в истинное распределение напряжении в детали.

По всем этим причинам понятие равнопрочности деталей относительно. Конструирование равнопрочных деталей практически сводится к прибли­зительному воспроизведению форм, диктуемых условием равнопрочности, при всемерном уменьшении влияния всех источников концентрации напря­жений.

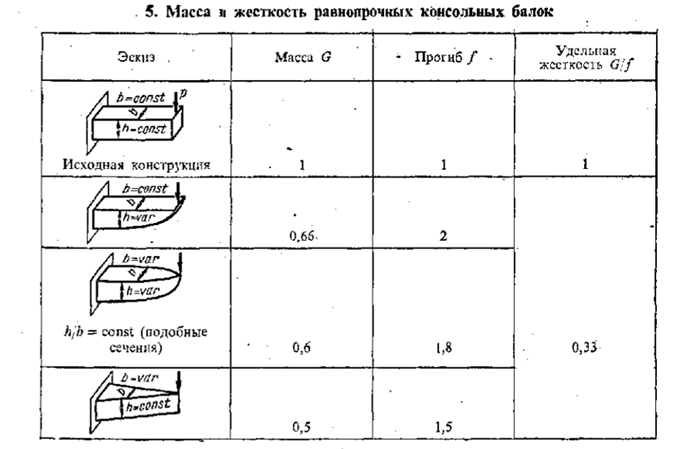
Выигрыш в массе от применения принципа равнопрочности зависит от типа нагружения и способа придания равнопрочности. Некоторое пред­ставление о порядке выигрыша в массе (а также снижения жесткости) дает пример консольных балок, нагруженных изгибающей силой Р (табл.5).

На рис. 33 представлены способы придания равнопрочности цилин­дрической детали, опертой по концам и подвергающейся изгибу попереч­ной силой, приложенной в средине пролета.

Дата добавления: 2014-12-26