
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ответ: Итак, совхоз должен приобрести 10 трехтонных и 5 пятитонных автомашин. В этом случае общая грузоподъемность составит 55 тонн
|
|
|
|
Задача №4
Заданные осциллограммы представить приближенно в виде суперпозиции гармоник. В разложении сохранить постоянное слагаемое и первые четыре гармоники. Найти коэффициенты разложения и начальные фазы гармоник. Для определения коэффициентов и фаз измерить и использовать ординаты точек на осциллограммах для 13 равноотстоящих значений абсциссы 0, 30, 60, 90, 120, 150, 180, 210, 240, 270, 300, 330 и 360 градусов. Измерения выполнить с точностью до двух значащих цифр, а вычисления – с точностью до трех значащих цифр. Построить график осциллограммы и найденного разложения.
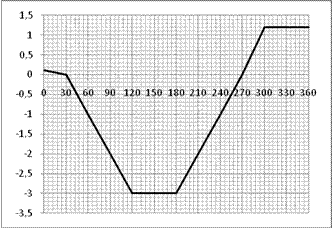
Рисунок 21 – График осциллограммы
Решение. Определим по графику ординаты для заданных значений абсциссы и запишем их в таблицу. В технике обычно углы измеряются в градусах, но в математике удобнее использовать радианы – для упрощения формул. Кроме того, большинство компьютерных программ общего назначения в тригонометрических функциях по умолчанию используют радианы в качестве меры угла. Поэтому значения x в таблице имеет смысл записать в радианах по формуле
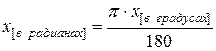 . (4)
. (4)
Таблица 5 – Заданные значения
| n | |||||||||||||
| x | 0,524 | 1,05 | 1,57 | 2,09 | 2,62 | 3,14 | 3,67 | 4,19 | 4,71 | 5,24 | 5,76 | 6,28 | |
| y | 0,11 | –1 | –2 | –3 | –3 | –3 | –2 | –1 | 1,2 | 1,2 | 1,2 |
Поскольку 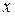 измеряется в радианах, причем
измеряется в радианах, причем 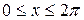 , формула для разложения функции в ряд Фурье имеет вид
, формула для разложения функции в ряд Фурье имеет вид
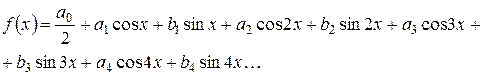 (5)
(5)
Коэффициенты разложения определяются по формулам
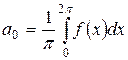 , (6)
, (6)
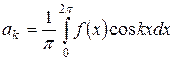 , (7)
, (7)
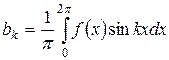 . (8)
. (8)
В нашей задаче аналитический вид функции 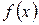 неизвестен, но мы нашли значения функции в нескольких точках, поэтому можем вычислить интегралы приближенно, например, по формуле трапеций:
неизвестен, но мы нашли значения функции в нескольких точках, поэтому можем вычислить интегралы приближенно, например, по формуле трапеций:
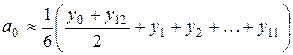 , (9)
, (9)
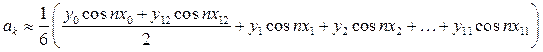 , (10)
, (10)
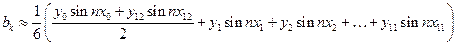 , (11)
, (11)
где 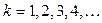
Все параметры в формулах (9–11) заданы в таблице 5, поэтому вычислим значения 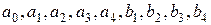 и заполним первые 3 столбца таблицы 6. Например, для
и заполним первые 3 столбца таблицы 6. Например, для 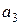 получим
получим
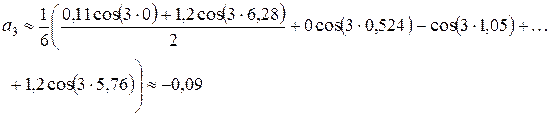
и т.д.
Таблица 6 – Парметры ряда Фурье
| k | 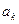
| 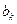
| 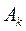
| 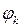
|
| –1,99 | ||||
| 1,85 | –1,12 | 2,2 | 2,12 | |
| –0,05 | –0,06 | 0,081 | –2,46 | |
| –0,09 | –0,03 | 0,096 | –1,88 | |
| –0,1 | 0,1 | –1,52 |
Во многих технических приложениях вместо суммы функций 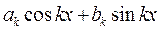 записывают одну функцию
записывают одну функцию 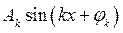 , которая представляет собой синусоиду с таким же периодом, но сдвинутую влево относительно
, которая представляет собой синусоиду с таким же периодом, но сдвинутую влево относительно 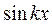 на
на 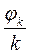 . Функцию
. Функцию 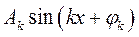 принято называть гармоникой. Ее параметры выражаются через
принято называть гармоникой. Ее параметры выражаются через 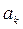 и
и 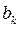 по формулам
по формулам
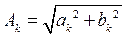 , (12)
, (12)
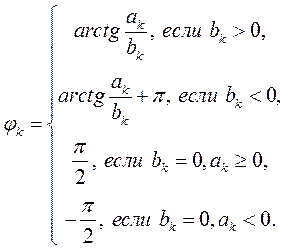 (13)
(13)
Если значение 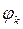 , вычисленное по формуле (13), превышает
, вычисленное по формуле (13), превышает 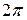 , то из него можно вычесть
, то из него можно вычесть 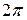 , так как синус – периодическая функция. С учетом формул (12, 13), формула (5) приобретает следующий вид
, так как синус – периодическая функция. С учетом формул (12, 13), формула (5) приобретает следующий вид
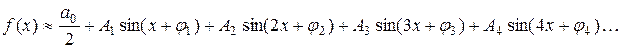 (11)
(11)
По формулам (12,13) заполним два последних столбца таблицы 6. Подставим найденные коэффициенты в формулу (14) и получим приближенное разложение в ряд Фурье для нашей осциллограммы
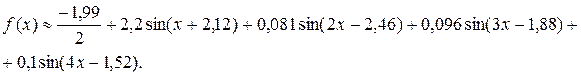 (15)
(15)
Для построения графика функции 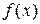 вычислим значения функции по формуле (15) для всех значений
вычислим значения функции по формуле (15) для всех значений 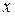 из таблицы 5.
из таблицы 5.
Таблица 7 – Значения функции по данным значениям аргумента
| n | |||||||||||||
| x | 0,524 | 1,05 | 1,57 | 2,09 | 2,62 | 3,14 | 3,67 | 4,19 | 4,71 | 5,24 | 5,76 | 6,28 | |
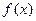
| 0,64 | 0,0001 | –0,95 | –2,2 | –2,9 | –3,1 | –2,9 | –2 | –1 | 0,069 | 1,2 | 1,3 | 0,64 |
Построим в одной системе координат график исходной осциллограммы и график ее разложения по гармоникам. Для этого построим точки с координатами из таблицы 5 и соединим их плавной линией черного цвета, затем построим точки с координатами из таблицы 7 и соединим их плавной линией синего цвета. При построении точек следует перевести абсциссы обратно в градусы по формуле
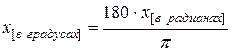
Полученный график показан на рисунке 22.
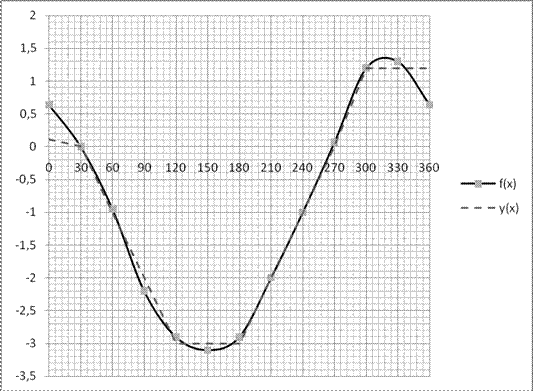
Рисунок 22 – Исходная осциллограмма и ее разложение в ряд Фурье
На этом графике 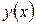 – исходная осциллограмма,
– исходная осциллограмма, 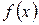 – ее разложение в ряд Фурье. Графики близки друг к другу при всех значениях x за исключением крайних точек
– ее разложение в ряд Фурье. Графики близки друг к другу при всех значениях x за исключением крайних точек 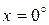 и
и 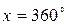 . Дело в том, что
. Дело в том, что 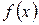 – функция непрерывная и периодическая, для нее
– функция непрерывная и периодическая, для нее 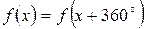 . В то же время, для нашей осциллограммы
. В то же время, для нашей осциллограммы 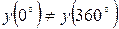 . Если ее график периодически продолжить на всю ось Оx, то точки
. Если ее график периодически продолжить на всю ось Оx, то точки 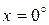 и
и 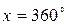 станут точками разрыва. В точках разрыва
станут точками разрыва. В точках разрыва 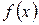 равно полусумме левостороннего и правостороннего пределов функции
равно полусумме левостороннего и правостороннего пределов функции 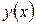 .
.
Задача №5
В задаче приведены данные по группе хозяйств о дозах внесения удобрений на 1 га посева зерновых в ц. (Х) и об урожайности зерновых культур в ц. с 1 га. (Y). Методом корреляционного анализа нужно исследовать зависимость меду этими признаками, построить корреляционное уравнение (уравнение регрессии), рассчитать коэффициент корреляции и построить график корреляционной зависимости. Сформулируем выводы корреляционного анализа.
Решение. Для решения следует составить вспомогательную таблицу.
Вспомогательная таблица для расчета коэффициентов регрессии и корреляции
| x | y | x2 | y2 | xy |
| 23.0 | ||||
| 1.1 | 1.21 | 27.5 | ||
| 2.9 | 8.41 | 87.0 | ||
| 3.9 | 15.21 | 140.4 | ||
| … | … | … | … | … |
| Суммы | ||||
| ∑x=35.5 | ∑y=216.6 | ∑x2=137.49 | ∑y2=5011.1 | ∑xy=827.31 |
Коэффициенты регрессии можно получить, составив и решив уравнения связь. Простейшим из них является уравнение прямой типа
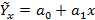
Для определения параметров уравнения а0 и а1 надо составить и решить систему нормальных уравнений с двумя неизвестными:
∑y=na0+a1∑x;
∑xy=a0∑x +a1∑x2.
Подставляя данные табл. VII в систему, получим:
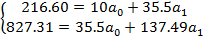
Освобождаемся от коэффициентов при а0, для чего первое уравнение делим на 10, второе — на 35.5:
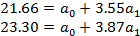
Из второго уравнения вычитаем и получим: 23,30—21.66=а0—а0+(3.87-3.55)а1, отсюда а1=5.125. Подставляя значение а1 в любое уравнение, получаем значение а0=3.47. Уравнение примет вид
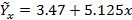
Коэффициент регрессии, равный 5.125 показывает, что с увеличением дозы внесения удобрений на единицу урожайности возрастает на 5.125 ц с 1 га в данных условиях.
Для расчета коэффициента корреляции целесообразно использовать формулу:
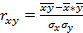 ,
,
Где
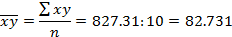
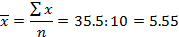
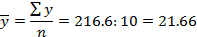
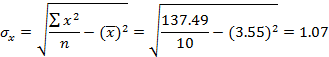
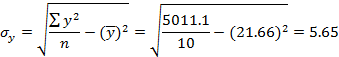
Тогда
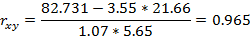
Ответ. rxy=0.965
Вывод: вязь между урожайностью и дозой внесения удобрений тесная, так как коэффициент корреляции близок к единице.
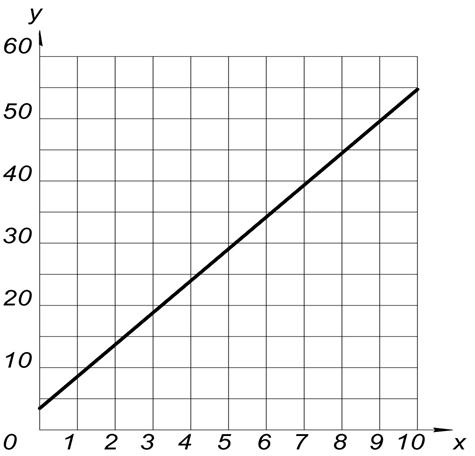
Для построения графика (прямой корреляционной зависимости) надо использовать полученное уравнение связи, поочередно подставляя в него значения «х», например:
Ух=3.47+5.125×1=8.595≈8.6;
Ух=3.47+5.125×1.1=9.107≈9.1;
Ух=3.47+5.125×2.9=18.332≈18.3 и т.д.
Затем на оси абсцисс откладываем значения «х» - факторного признака, на оси ординат – результативного признака 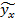 и соответствующие точки, находящиеся на пересечении этих признаков, соединяются прямой линией.
и соответствующие точки, находящиеся на пересечении этих признаков, соединяются прямой линией.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 562; Нарушение авторских прав?; Мы поможем в написании вашей работы!