Основы теории плавания тел

Гидростатический парадокс

Рассмотрим три сосуда разной формы, заполненные жидкостью до одного уровня h_c. Все сосуды такие, что имеют одинаковую площадь дна.

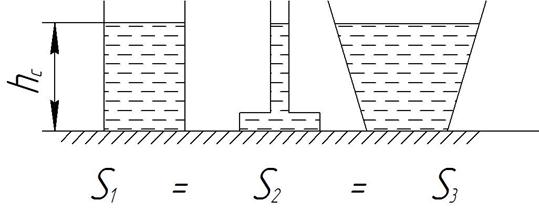
Рисунок 19 – Гидростатический парадокс

В соответствии с общей формулой определения силы, действующей на плоскую поверхность

,

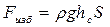можно вычислить силу, действующую на дно сосуда. Для всех трёх сосудов эти силы окажутся одинаковыми и независящими от веса жидкости в сосуде. Но на опору все сосуды будут действовать с разными силами, равными весу сосудов с жидкостью. Этот факт получил название гидростатического парадокса.

Будем считать, что в жидкость плотностью ρ погружено тело объёмом V. Выберем систему координат, ось Z которой направим вниз, а оси X и Y вдоль свободной поверхности. Рассмотрим усилия, действующие на тело со стороны жидкости. Все горизонтальные составляющие, как было установлено выше, будут уравновешиваться. Для определения вертикальных составляющих выделим в твёрдом теле элементарный цилиндрический объём с площадью поперечного сечения dS. На торцевые поверхности этого объёма действуют силы dF₁ сверху и dF₂ снизу.

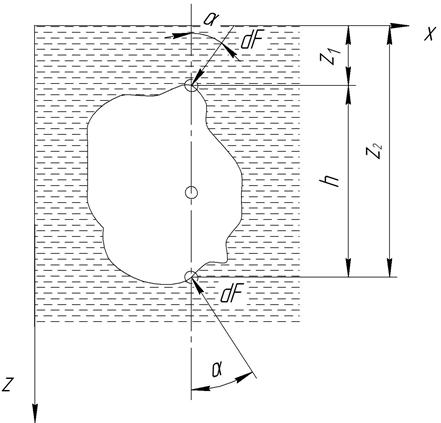
Рисунок 20 – Основы теории плавания тел

Вертикальная составляющая силы dF₁ будет:

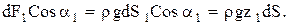
Вертикальная составляющая силы dF₂ будет:

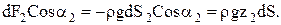
Будем считать, что погруженное в жидкость тело находится в равновесии. Поэтому вес выделенного элементарного цилиндра dG будет уравновешиваться действующими на него силами.

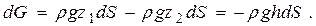
Проинтегрировав это выражение по площади горизонтальной проекции тела, получим:

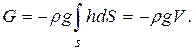(59)

Это выражение называется законом Архимеда: погруженное в жидкость тело теряет в своём весе столько, сколько весит вытесненная им жидкость. Другими словами на тело, погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной телом жидкости. Эта сила приложена в точке, которая называется точкой водоизмещения.

В зависимости от отношения веса и выталкивающей силы возможны три состояния тела:

Ø если вес больше выталкивающей силы – тело тонет,

Ø если вес меньше выталкивающей силы – тело всплывает,

Ø если вес равен выталкивающей силе – тело плавает.

Она направлена вертикально вверх и приложена в точке, соответствующей центру давления называемому - центром водоизмещения, количество воды, вытесненной плавающим телом, — водоизмещением.

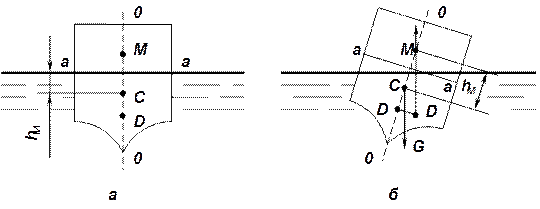
Рисунок 21 - Плавучесть тела а и 6 — cудно остойчиво

На рисунке 21 показана схема корпуса судна со следующи­ми обозначениями: а—а—плоскость плавания, ограниченная ватерлинией, как контуром; о—о— ось плавания—ось, нормаль­ная к плоскости плавания и проходящая через центр тяжести тела С.

На оси плавания расположены три центра: центр тяжести С, центр водоизмещения D и метацентр М (точка пересечения оси плавания с линией действия архимедовой силы).

Расстояние от метацентра до центра тяжести тела называют метацентрической высотой h_м. Приняв за плоскость сравнения – плоскость плавания охарактеризуем остойчивость.

При h_м > 0 положение тела будет остойчивым, при h_м < 0 — неостойчивым, а при h_м =0 тело будет находиться в состоянии безразличного равновесия.

Плавучесть и остойчивость — ключевые понятия теории плава­ния тел. Плавучесть — это состояние равновесия твердого тела, частично или полностью погру­женного в жидкость. Остойчи­вость — способность плаваю­щего тела, выведенного из рав­новесия, восстанавливать исходное положение после прекращения действия сил, вызывающих крен. Крен — положение тела, при котором вертикальная плоскость его симметрии отклонена от вертикали к земной поверхности.

Между соотношениями веса плавающего тела G и его вытал­кивающей силой Рв возможны три состояния тела, погруженного в жидкость.

Если G > Рв, то тело тонет, так как равнодействую­щая сил G и Рв направлена вертикально вниз.

Если G < Рв, тело плавает в полупогруженном состоянии (надводное плавание), и при этом равнодейст­вующая сил G и Рв направлена вертикально вверх, поэтому тело всплывает, пока новая уменьшенная выталкивающая сила Рв не будет равна весу тела G (G=Pv).

Тело плавает в погруженном состоянии в случае G=Pв, оно может находиться в устойчивом или неустойчивом равновесии. Чтобы тело находилось в равно­весии, необходимо, чтобы его центр тяжести и центр водоизме­щения лежали на одной вертикали.

В случае воздействия на плавающее тело внешних сил (ветра, крутого поворота) оно будет отклоняться от положения равнове­сия (давать крен). При остойчивом плавании тела центр тяжести расположен ниже центра водоизмещения, а после прекращения взаимодействия этих сил тело возвращается в прежнее положе­ние. При неостойчивом плавании центр тяжести тела располо­жен выше центра водоизмещения, В этом случае тело выведено из состояния равновесия и не может возвратиться в первона­чальное положение. Состояние безразличного равновесия харак­теризуется совпадением центров тяжести и водоизмещения.

Плавучесть тела выражается формулой

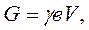
где G вес воды; gв — удельный вес воды; V — объем вытесненной телом воды.

Дата добавления: 2014-12-26