Угловые характеристики синхронного генератора

Электромагнитная мощность неявнополюсного синхронного генератора при его параллельной работе с сетью

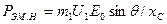(21.7)

где 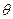- угол, на который продольная ось ротора смещена относительно продольной оси результирующего поля машины (рис. 21.4).

Электромагнитная мощность явнополюсного синхронного генератора

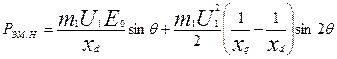(21.8)

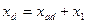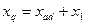где и — синхронные индуктивные сопротивления явнополюсной синхронной машины по продольно и поперечной осям соответственно, Ом.

Разделив выражения (21.7) и (21.8) на синхронную угловую скорость вращения 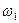, получим выражения электромагнитных моментов:

неявнополюсной синхронной машины

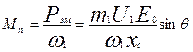(21.9)

явнополюсной синхронной машины

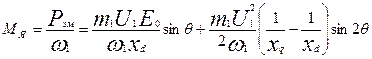(21.10)

где М — электромагнитный момент, Нм.

Анализ выражения (21.10) показывает, что электромагнитный момент явнополюсной машины имеет две составляющие: одна из них представляет собой основную составляющую электромаг­нитного момента

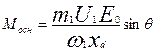. (21.11)

другая — реактивную составляющую момента

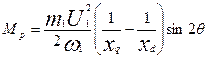. (21.12)

Основная составляющая электромагнитного момента 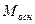яв­нополюсной синхронной машины зависит не только от напряже­ния сети ( 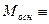U₁), но и от ЭДС 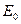, наведенной магнитным по­током вращающегося ротора 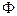в обмотке статора:

.(21.13)

Это свидетельствует о том, что основная составляющая электро­магнитного момента 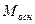зависит от магнитного потока ротора: 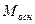≡ 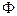. Отсюда следует, что в машине с невозбужденным рото­ром ( 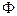= 0) основная составляющая момента 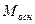= 0.

Реактивная составляющая электромагнитного момента 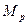не зависит от магнитного потока полюсов ротора. Для возникновения этой составляющей достаточно двух условий: во-первых, чтобы ротор машины имел явновыраженные полюсы (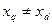) и, во-вторых, чтобы к обмотке статора было подведено напряжение сети ( 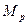≡ 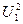). Подробнее физическая сущность реактивного момента будет изложена в § 23.2.

При увеличении нагрузки синхронного генератора, т. е. с ростом тока I₁ происходит увеличение угла 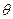, что ведет к изменению электромагнитной мощности генератора и его электромагнитного момента. Зависимост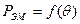и и 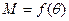, представленные графически, называются угловыми характеристиками синхронной машины.

Рассмотрим угловые характеристики электромагнитной мощности 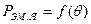и электромагнитного момента 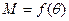явнополюсного синхронного генератора (рис. 21.5). Эти характеристики построены при условии постоянства напряжения сети (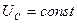) и магнитного потока возбуждения, т. е. 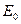= const. Из выражений (21.8) и (21.11) видим, что основная составляющая электромагнитного момента 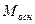и соответствующая ей составляющая электромагнитной мощности изменяются пропорционально сину­су угла 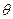(график 1), а реактивная составляющая момента (21.12) и соответствующая ей составляющая электромагнитной мощности изменяется пропорционально синусу угла 2 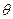(график 2). Зависимость результирующего момента 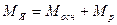и электромагнитной мощности 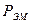от угла 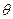определяется графиком 3, полученным сложением значений моментов 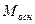и 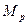и соответствую­щих им мощностей по ординатам.

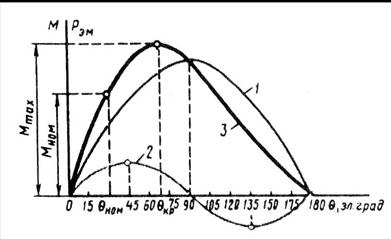
Рис. 21.5. Угловая характеристика синхронного генератора.

Максимальное значение электромагнитного момента 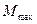со­ответствует критическому значению угла .

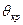Как видно из результирующей угловой характеристики (гра­фик 3), при увеличении нагрузки синхронной машины до значе­ний, соответствующих углу 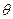≤ 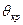, синхрон­ная машина работает устойчиво. Объясняется это тем, что при 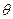≤ 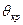, рост нагрузки генерато­ра (увеличение 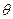) со­провождается увеличе­нием электромагнитно­го момента. В этом слу­чае любой установив­шейся нагрузке соответ­ствует равенство враща­ющего момента первичного двигателя 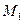сумме противодействую­щих моментов, т. е. 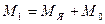. В результате частота вращения ротора остается неизменной, равной синхронной частоте вращения.

При нагрузке, соответствующей углу 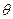> 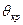, электромагнит­ный момент M _я, уменьшается, что ведет к нарушению равенства вращающего и противодействующих моментов. При этом избы­точная (неуравновешенная) часть вращающего момента первично­го двигателя 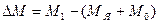вызывает увеличение частоты вращения ротора, что ведет к нарушению условий синхронизации (машина выходит из синхронизма).

Электромагнитный момент, соответствующий критическому значению угла (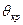), является максимальным М _mах.

Для явнополюсных синхронных машин 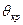= 60÷80 эл. град. Угол 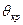можно определить из формулы

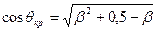(21.14)

Здесь

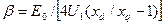. (21.15)

У неявнополюсных синхронных машин 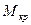= 0, а по­этому угловая характеристика представляет собой синусоиду и угол 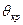= 90°.

Отношение максимального электромагнитного момента М_max к но­минальному 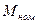называется перегрузочной способностью синхронной машины или коэффициентом статической перегружаемости:

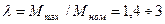. (21.16)

Пренебрегая реактивной составляющей момента, можно записать

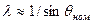, (21.17)

т.е. чем меньше угол 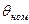, соответствующий номинальной на­грузке синхронной машины, тем больше ее перегрузочная способ­ность. Например, у турбогенератора 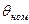= 25 ÷ 30°, что соответст­вует = 2,35÷2,0.

Пример 21.1. Трехфазный синхронный генератор с явно выраженными по­люсами на роторе (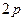 =10) включен на параллельную работу с сетью напряжени­ем 6000 В частотой 50 Гц. Обмотка статора соединена звездой и содержит в каж­дой фазе = 310 последовательных витков, обмоточный коэффициент 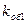= 0,92, индуктивное сопротивление рассеяния обмотки 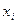= 10 Ом. Диаметр расточки D₁ = 0,8 м, расчетная длина сердечника статора l_i = 0,28 м, воздушный зазор рав­номерный δ = 2 мм, коэффициент полюсного перекрытия =0,7, коэффициент воздушного зазора k_δ = 1,3, коэффициент магнитного насыщения 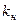= 1,1. Маг­нитный поток ротора Ф = 0,058 Вб.

Требуется рассчитать значения электромагнитных моментов и построить графики 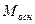, 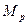и М = f().

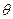Решение. Полное индуктивное сопротивление реакции якоря по (20.19)

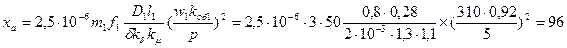Ом

При 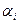= 0,7 и равномерном зазоре коэффициенты формы поля по (20.7) и (20.8):

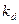= 0,958 и 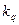= 0,442.

Индуктивное сопротивление реакции якоря по продольной оси [см. (20.24)]

Ом,

по поперечной оси [см. (20.25)]

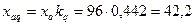Ом.

Синхронные индуктивные сопротивления по продольной и поперечной осям:

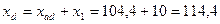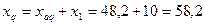Ом,

Ом.

ЭДС обмотки статора в режиме х.х. по (21.13)

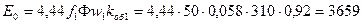В.

Напряжение фазы обмотки статора

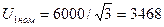В.

Угловая частота вращения ротора

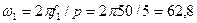с^-1.

Максимальное значение основной составляющей электромагнитного момента генератора (21.11)

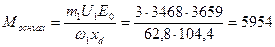Н∙м

Максимальное значение реактивной составляющей электромагнитного момента (21.12)

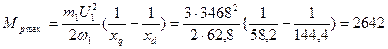Н·м

Результаты расчета моментов

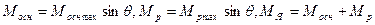для ряда значений угла 0 приведены ниже:

,град
s in	0,342	0,500	0,707	0,866	0,940	1,0
, Нм
sin 2	0,643	0,866	1,0	0,866	0,643
Mp, Нм
M,Нм

Угол 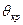, соответствующий максимальному моменту 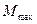, по (21.14)

,

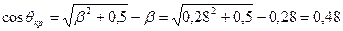где ;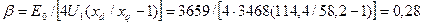

0,48 = 61,3°.

Углу 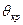= 61,3° соответствуют моменты:

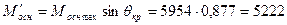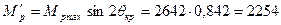Н∙м;

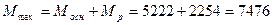Н∙м;

Н∙м.

Графики моментов 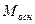, 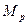и 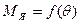, построенные по результатам рас­чета, приведены на рис 21.6.

Дата добавления: 2014-12-27