ВВЕДЕНИЕ 2 страница. Решение типового варианта

Решение типового варианта

Методику выполнения этого задания покажем на результатах задания 1.

1. По виду гистограммы и полигона частостей (напоминают нормальную кривую), а также по значению выборочных коэффициентов асимметрии и эксцесса (А_s(X)=0,749, , они близки к нулю), предполагая, что СВ Х – стоимость основных производственных фондов изменяется под влиянием большого числа факторов, примерно равнозначных по силе влияния, можно выдвинуть гипотезу о том, что закон распределения СВ Х является нормальным.

2. Плотность вероятности нормального закона распределения имеет вид , или

Точечными оценками параметров а и s нормального закона распределения служат средняя выборочная и среднее выборочное квадратическое отклонение , вычисленные ранее, т.е. , 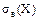=0,251. Следовательно, плотность вероятности предполагаемого нормального закона распределения имеет вид

, или

.

Функция распределения предполагаемого нормального закона

.

Используя нормированную функцию Лапласа , функцию распределения нормального закона записывают в виде 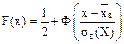, в нашем случае эта функция есть 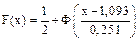, ее называют теоретической функцией распределения.

3. Проведем проверку гипотезы о нормальном законе распределения СВ Х, используя критерий согласия Пирсона . Для удобства вычислений интервалы наблюденных значений нормируют, т.е. выражают их в единицах среднего квадратического отклонения : , причем наименьшее значение u_i полагают равным , а наибольшее – , эта замена производится для того, чтобы сумма теоретических частот была равной объему выборки. Далее вычисляют вероятность попадания СВ Х, распределенной по нормальному закону с параметрам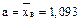и и , в частичные интервалы по формуле

После того как будут найдены находим теоретические частоты для каждого частичного интервала по формуле , где – теоретическая частота i-го интервала. Между теоретическими и эмпирическими частотами могут быть расхождения. Замену эмпирических частот теоретическими называют выравниванием частот статистического ряда.

Составим табл. 8 для вычисления теоретических частот СВ Х.

Для примера вычислений найдем вероятность того, что СВ Х попадет в первый частичный интервал , эта вероятность равна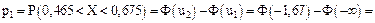

. Аналогично находим

и т.д. Для вычисления значений функции Ф использовано приложение 1. После этого вычисляют теоретические частоты , например, и т.д. Сумма теоретических частот должно быть равна объему выборки, т.е. . Далее находим значение выборочной статистики или это есть наблюдаемое значение критерия . Затем по таблицам квантилей распределения , по уровню значимости =0,05 и числу степеней свободы (где k – число частичных интервалов, r – число параметров предполагаемого закона распределения СВ X) находят критическое значение 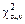, удовлетворяющее условию . При использовании критерия необходимо, чтобы в каждом частичном интервале было не менее 5 элементов. Если же число элементов менее 5, рекомендуется соседние интервалы объединять в один (как это сделано в табл.9). Уменьшенное число частичных интервалов учитывается при нахождении числа степеней свободы .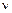

Составим табл. 9 для вычисления .

Т а б л и ц а 9. Вычисление выборочной статистики CВ Х

Интервалы наблюдаемых значе- ний СВ Х	Эмпирические частоты	Теоретические частоты
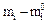
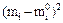
0,465–0,675   0,675–0,885   0,885–1,095   1,095–1,305   1,305–1,515   1,515–1,725   1,725–1,935	3 17	4,75 20,33 15,58   30,07   29,55   15,40   4,06 20,05   0,59	– 1,33     7,93   – 3,55   – 3,05	1,7689     62,8849   12,6025   9,3025	0,0870     2,0913   0,4264   0,4640
Сумма

Т а б л и ц а 8. Вычисление теоретических частот СВ Х

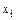
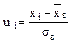
Интервалы наблюденных значений СВ Х	Частоты mi	Начало интервала	Конец интервала						Теоретические частоты
0,465–0,675		0,465	0,675	–	– 1,67	– 0,5	–0,4525	0,0475	4,75
0,675–0,885		0,675	0,885	– 1,67	– 0,83	– 0,4525	–0,2967	0,1558	15,58
0,885–1,095		0,885	1,095	– 0,83	0,01	– 0,2967	–0,0040	0,3007	30,07
1,095–1,305		1,095	1,305	0,01	0,84	0,0040	0,2995	0,2955	29,55
1,305–1,515		1,305	1,515	0,84	1,68	0,2995	0,4535	0,1540	15,40
1,515–1,725		1,515	1,725	1,68	2,52	0,4535	0,4941	0,0406	4,06
1,725–1,935		1,725	1,935	2,52	+	0,4941	0,5	0,0059	0,59
Сумма

Число степеней свободы По таблице квантилей (приложение 2) по уровню значимости и числу степеней свободы 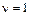находим критическое значение Так как то нет оснований для отклонения гипотезы о нормальном законе распределения СВХ. Другими словами расхождения между эмпирическими и теоретическими частотами являются незначительными, т.е. случайными и предположение о распределении СВ Х по нормальному закону вполне согласуется с эмпирическим распределением выборки.

На рис.5 построены нормальная кривая по найденным теоретическим частотам и полигон эмпирических (наблюдаемых) частот.

4. Доверительный интервал для оценки математического ожидания случайной величины Х, распределенной по нормальному закону, (при n 30) находят по формуле

где квантили нормального распределения 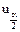находят по таблицам функции Лапласа (приложение 1) из условия – доверительная вероятность, в нашем случае 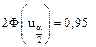или и Точность оценки математического ожидания (предельная погрешность) есть 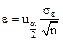. Вычислим предельную погрешность 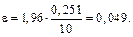Искомый доверительный интервал, накрывающий математическое ожидания СВ Х, равен

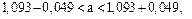
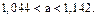
Рис. 5.

Смысл полученного результата таков: если будет произведено достаточно большое число выборок по 100 значений СВ Х – стоимости основных производственных фондов, то в 95% из них доверительный интервал накроет математическое ожидание СВ Х и только в 5% случаев математическое ожидание может выйти за границы доверительного интервала.

Аналогичным образом выполним это задание для СВ У – стоимость валовой продукции (у. е /га).

1. По виду гистограммы и полигона частостей, а также по значению выборочных коэффициентов асимметрии и эксцесса ( выдвигаем гипотезу о том, что закон распределения СВ У является нормальным.

2. Плотность вероятности предполагаемого нормального закона распределения имеет вид

Функция распределения нормального закона для СВ У есть .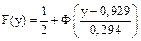

3. Вычислим теоретические частоты нормального распределения СВ У для проверки согласия эмпирической функции распределения с теоретической (табл.10).

Далее составим табл. 11 для нахождения выборочной статистики СВ У.

Число степеней свободы . По таблице (приложение 2) по уровню значимости находим критическое значение . Так, как , то нет оснований для отклонения гипотезы о нормальном законе распределения СВ У.

На рис. 6 построены эмпирическая и теоретическая кривые распределения.

4. Для нахождения доверительного интервала для оценки математического ожидания СВ У вычислим предельную погрешность , тогда доверительный интервал равен 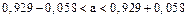или .

Рис. 6.

Т а б л и ц а 11. Вычисление выборочной статистики СВ У

Интервалы наблюдаемых значе- ний СВ У	Эмпирические частоты	Теоретические частоты
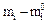
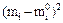
0,39–0,61   0,61–0,83   0,83–1,05   1,05–1,27   1,27–1,49   1,49–1,71   1,71–1,93	3 13	14,01   22,68   29,22   21,79   9,49   2,42 12,3   0,39	– 0,1   3,32   – 0,22   – 3,79   0,7	0,01   11,0224   0,0484   14,3641   0,49	0,0007   0,4860   0,0017   0,6592   0,0398
Cумма

Задание 3. КОРРЕЛЯЦИЯ

1. По результатам задания 1 составить корреляционную таблицу.

2. Найти условные средние 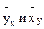, построить точки , и по характеру их расположения подобрать вид функций регрессии.

3. Найти выборочный коэффициент корреляции и сделать вывод о силе корреляционной связи.

4. Найти доверительный интервал, накрывающий коэффициент корреляции генеральной совокупности с заданной доверительной вероятностью .

5. Найти уравнения линий регрессии х на у и у на х и построить их.

Решение типового варианта

Методику выполнения этого задания покажем на примере статистических данных табл.1, где СВ Х – стоимость основных производст-

венных фондов (у. е /га), СВ У – стоимость валовой продукции (у.е/га).

1. Для составления корреляционной таблицы воспользуемся разбиением СВ Х и У на частичные интервалы (табл. 2 и 5). Сделаем подсчет частот системы СВ Х и У, рассматривая каждую пару значений табл.1. Например, первая пара (0,73; 0,60) попадает во вторую строку и первый столбец табл.8 и отмечается черточкой. Вторая пара значений (0,82; 0,61) попадает также во вторую строку и первый столбец, причем, значение 0,61 совпадает с концами интервалов 0,39–0,61 и 0,61–0,83; будем относить это число к тому интервалу, где наблюдается совпадение с правым концом, т.е. к интервалу 0,39–0,61. Третья пара (0,89; 0,95) – третья строка и третий столбец. Таким образом просматриваем все 100 пар значений системы СВ Х и У. В результате получим табл. 12.

Т а б л и ц а 12. Подсчет частот системы СВ Х и У

У Х	0,39–0,61	0,61–0,83	0,83–1,05	1,05–1,27	1,27–1,49	1,49–1,71	1,71–1,93
0,465–0,675		I
0,675–0,885	IIIIIIII	IIIIII	III	I
0,885–1,095	IIIIII	IIIIIIIII IIIIII	IIIIIIIII IIII	III	I
1,095–1,305		IIII	IIIIIIIIII	IIIIIIIII	II	I
1,305–1,515			II	III	IIII	II
1,515–1,725					II		I
1,725–1,935			I	II

Для дальнейших расчетов нужны будут середины интервалов, которые запишем под частичными интервалами.

Т а б л и ц а 10. Вычисление теоретических частот СВ У

Интервалы наблюденных значений СВ У	Частоты   mi	Начало ин- тервала	Конец интер-вала						Теоретичес кие час- тоты
0,39–0,61		0,39	0,61	–	– 1,8	–0,5	–0,3599	0,1401	14,01
0,61–0,83		0,61	0,83	– 1,08	– 0,34	–0,3599	–0,1331	0,2268	22,68
0,83–1,05		0,83	1,05	– 0,34	0,41	–0,1331	0,1591	0,2922	29,22
1,05–1,27		1,05	1,27	0,41	1,16	0,1591	0,3770	0,2179	21,79
1,27–1,49		1,27	1,49	1,16	1,91	0,3770	0,4719	0,0949	9,49
1,49–1,71		1,49	1,71	1,91	2,66	0,4719	0,4961	0,0242	2,42
1,71–1,93		1,71	1,93	2,66	+	0,4961	0,5	0,0039	0,39
Сумма

В столбце табл.13 записаны суммы частот по строкам, а в строке – суммы частот по столбцам. , где n – объем выборки.

2. Находим условные средние по формуле

;

;

;

Т а б л и ц а 13. Корреляционная таблица системы СВ Х и У

У Х	0,39– 0,61 0,50	0,61– 0,83 0,72	0,83– 1,05 0,94	1,05– 1,27 1,16	1,27– 1,491,38	1,49– 1,71 1,60	1,71–1,93 1,82
0,465–0,675 0,57
0,675–0,885 0,78
0,885–1,095 0,99
1,095–1,305 1,20
1,305–1,515 1,41
1,515–1,725 1,62
1,725–1,935 1,83

;

;

;

;

.

Результаты вычислений заносим в табл. 14.

Т а б л и ц а 14. Условные средние

Дата добавления: 2014-12-23