Анализ сетей Петри

Пример сети Петри для системы обнаружения и устранения неисправностей в технической системе

Пример 2. Требуется описать с помощью сети Петри процессы возникновения и устранения неисправностей в некоторой технической системе, состоящей из М однотипных блоков; в запасе имеется один исправный блок; известны статистические данные об интенсивностях возникновения отказов и длительностях таких операций, как поиск неисправностей, замена и ремонт отказавшего блока.

На рис. 5.17 представлена соответствующая сеть Петри. При числе маркеров в позиции, равном М, можно не ставить М точек, а записать в позиции значение М.

В данном примере значение М в позиции p₂ соответствует числу имеющихся в системе блоков. Переходы отображают следующие события: t₁ – отказ блока, t₂ – обнаружение неисправного блока, t₃ – замена неисправного блока, t₄ – окончание ремонта.

При наличии маркера в позиции p₂ переход t₁ срабатывает, но с задержкой, равной вычисленному случайному значению моделируемого отрезка времени между отказами. После выхода маркера из t₁ он попадает через p₁ в t₂, если имеется маркер в позиции p₆. Это означает, что обслуживающая систему бригада специалистов свободна и может приступать к поискувозникшей неисправности.

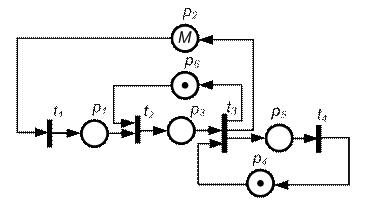
Рис. 5.17. Сеть Петри к примеру 2

В переходе t₂ маркер задерживается на время, равное случайному значению длительности поиска неисправности. Далее маркер оказывается в р₃, и, если имеется запасной блок (маркер в р₄), то запускается переход t₃, из которого маркеры выйдут в p₂, p₅ и p₆, через отрезок времени, требуемый для замены блока. После этого в t₄ имитируется восстановление неисправного блока.

Анализ сложных систем на базе сетей Петри можно выполнять посредством имитационного моделирования СМО, представленных моделями сетей Петри. При этом задают входные потоки заявок и определяют соответствующую реакцию системы. Выходные параметры СМО рассчитывают путем обработки накопленного при моделировании статистического материала.

Возможен и другой подход к использованию сетей Петри для анализа объектов, исследуемых на системном уровне. Он не связан с имитацией процессов и основан на исследовании таких свойств сетей Петри, как ограниченность, безопасность, сохраняемость, достижимость, живость.

Ограниченность (или К-ограниченность) имеет место, если число меток в любой позиции сети не может превысить значения К. При проектировании автоматизированных систем определение К позволяет обоснованно выбирать емкости накопителей. Возможность неограниченного роста числа меток свидетельствует об опасности неограниченного роста длин очередей.

Безопасность— частный случай ограниченности. Конкретно безопасность соответствует 1-ограниченности. Если для некоторой позиции установлено, что она безопасна, то ее можно представлять одним триггером.

Сохраняемость характеризуется постоянством загрузки ресурсов, т.е.

где N_i – число маркеров в i- й позиции; A_i – весовой коэффициент.

ДостижимостьМ_k → М_j характеризуется возможностью достижения маркировки М_j из состояния сети, характеризуемого маркировкой М_k.

Живость сети Петри определяется возможностью срабатывания любого перехода при функционировании моделируемого объекта. Отсутствие живости означает либо избыточность аппаратуры в проектируемой системе, либо свидетельствует о возможности возникновения зацикливаний, тупиков, блокировок.

В основе исследования перечисленных свойств сетей Петри лежит анализ достижимости.

Один из методов анализа достижимости любой маркировки из состояния М₀ – построение графа достижимости. Начальная вершина графа отображает М₀, а остальные вершины соответствуют маркировкам. Дуга из М_i, в М_j означает событие М_i → М_j и соответствует срабатыванию перехода t. В сложных сетях граф может содержать чрезмерно большое число вершин и дуг. Однако при построении графа можно не отображать все вершины, так как многие из них являются дублями (действительно, от маркировки М_k всегда порождается один и тот же подграф вне зависимости от того, из какого состояния система пришла в М_k).

На рис. 5.18 показана сеть Петри к примеру с одной рабочей станцией и N пользователями. Граф достижимости для данной сети показана на рис. 5.19.

Рис. 5.18. Сеть Петри к примеру 1

На рисунке 5.19 вершины графа изображены в виде маркировок, дуги помечены срабатывающими переходами. Данная сеть явно обладает свойством живости, так как срабатывают все переходы, а тупики отсутствуют.

Рис. 5.19. Граф достижимости сети Петри к примеру 1

Пример 3. Сеть Петри для двухпроцессорной вычислительной системы с общей памятью и ее граф достижимости представлены на рис. 5.20. Сеть является живой: все разметки достижимы.

Рис. 5.20. Сеть Петри и ее граф достижимости к примеру 2

Вопросы к разделу 5.2

1. Что такое N -схемы?
2. Для чего используют сети Петри?
3. Что такое маркировка сети Петри?
4. Какая из разновидностей сетей Петри приводит практически к тем же результатам моделирования, что и теория массового обслуживания?
5. Чем вызваны возможные конфликтные ситуации в N-схемах?
6. В чем заключается анализ достижимости сетей Петри?
7. Как строится граф достижимости сети Петри?

Дата добавления: 2014-12-27