Оценка эффективности многоканальной СМО

Рассмотрим многоканальную СМО,в которой выполняются следующие требования.

· На вход системы поступает простейший поток заявок;

· Каждый канал обслуживает одну заявку;

· Время обслуживания подчиняется показательному закону;

· Если хотя бы один канал свободен, то заявка принимается на обслуживание;

· Заявка теряется, если поступает в тот момент, когда все каналы заняты, т.е. другими словами это система с отказами.

Рассмотрим следующие критерии эффективности работы СМО:

1) вероятность отказа в обслуживании P_отк;

2) относительная пропускная способность π₀;

3) абсолютная пропускная способность π.

Обозначим состояния системы соответствующими вероятностями (табл. 6):

Таблица 6

Состояние СМО	Описание состояния	Вероятность
	Все каналы свободны	P0(t)
	1 канал занят	P1(t)
.......	........	....
N	Все каналы заняты	Pn(t)= Pотк

Ф о р м у л а Э р л а н г а

Чтобы получить выражение для исходных критериев необходимо составить систему дифференциальных уравнений, связывающую вероятности предыдущих и последующих состояний СМО (уравнений Колмогорова) и, затем, решить эту систему.

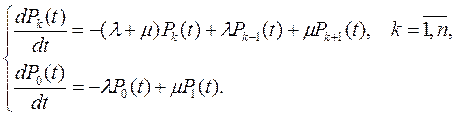
На практике часто представляет интерес установившийся процесс, описываемый стационарным решением указательной системы дифференциальных уравнений при t→∞.

При этом, для всех индексов k, от 1 до n производные равны нулю и система дифференциальных уравнений превращается в систему алгебраических уравнений Колмогорова:

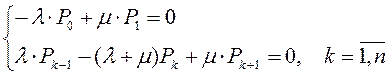
Решением подобной системы уравнений для случая n обслуживающих аппаратов является формула Эрланга, выражающая предельные вероятности состояний P_k:

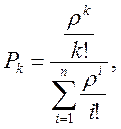
где ρ – нормированная интенсивность входного потока заявок (загрузка обслуживающего прибора).

Формула Эрланга дает вероятность того, что k каналов из n заняты обслуживанием заявок.

К р и т е р и и э ф ф е к т и в н о с т и р а б о т ы м н о г о к а н а л ь н о й СМО

С помощью формулы Эрланга найдем выражения для введенных критериев.

Вероятность отказа в обслуживании – вероятность того, что в момент прихода заявки все обслуживающие приборы будут заняты (в формуле Эрланга k = n):

Относительная пропускная способность – вероятность обслуживания:

Абсолютная пропускная способность – количество заявок в единицу времени:

П р и м е р о ц е н к и э ф ф е к т и в н о с т и р а б о т ы

м н о г о к а н а л ь н о й СМО

Рассмотрим работу участка токарных станков.

Участок включает 3 одинаковых станка со среднем временем обработки одной детали 3 минуты.

Детали приходят на участок в среднем через 2 минуты.

Требуется определить вероятность отказа, а также относительную и абсолютную пропускную способность участка.

Решение

Три станка на участке означает, что n= 3.

1. Определим среднюю скорость поступления заявок (деталей):

λ= 1/2 [мин^-1].

2. Определим среднюю скорость обслуживания: μ= 1/3 [мин^-1].

3. Найдем величину загрузки обслуживающего прибора (станка):

ρ= λ/ μ= 3/2 = 1,5.

Если бы на участке был только один станок с такой загрузкой ρ> 1, то, как известно из теории, он не справился бы с таким потоком деталей, и число отказов неограниченно возрастало бы (если учитывать очередь, то она возрастала бы до бесконечности L→∞).

4. Найдем вероятность отказа в обслуживании для трех станков, используя формулу Эрланга:

Это означает, что в среднем из 100 поступающих на обработку деталей 17 (точнее: из 1000 – 176) могут быть не приняты (отправлены назад, например, в тару), так как в это время все 3 станка заняты обработкой других деталей.

5. Найдем относительную пропускную способность (вероятность обслуживания):

π₀ =1 – P₃= 1 – 0,17647=0,82353.

Это означает, что в среднем из 100 поступающих на участок деталей примерно 82 будут обработаны.

6. Определим абсолютную пропускную способность:

π = λ·π₀ =0,5·0,82353·60=24,7059[дет/час].

Заметим, что если бы детали приходили на участок не случайным образом, а регулярно, т.е. строго каждые 2 минуты, то все детали на участке успевали бы обрабатываться, и даже еще оставалось бы время, т.е. никаких отказов бы не было! Это следует из того, что среднее время обработки одной детали участком из трех станков равно:

μ₃=( 1/3 ) · 3 = 1[мин^-1] → Т₃=1/ μ₃= 1 [мин].

Возможности оценки характеристик СМО с использованием аналитических моделей теории массового обслуживания ограничены по сравнению с теми требованиями, которые предъявляют практические задачи, возникающие при исследовании и проектировании реальных систем.

Вопросы к разделу 5.1

1. Что такое Q-схемы?
2. Почему модели систем массового обслуживания относят к аналитическим?
3. Почему на практике сложные модели СМО стараются не использовать?
4. Что служит альтернативой использования моделей массового обслуживания?
5. Для чего используются дисциплины обслуживания?
6. Какой поток заявок называется простейшим?
7. Какие распределения вероятностей традиционно используются для описания простейшего потока заявок?
8. Почему функции многомерного распределения вероятностей Пуассона имеют экстремумы?
9. Какие распределения вероятностей чаще всего используются для описания времени обслуживания?
10. Какие существуют способы согласования источника заявок с обслуживающими аппаратами?
11. Какими показателями характеризуется качество обслуживания?
12. Какие выводы можно сделать в зависимости от величины коэффициента загрузки обслуживающего аппарата?
13. Какие критерии эффективности СМО позволяет оценить формула Эрланга?

Дата добавления: 2014-12-27