Приклад кодування Хафмана

Кодування Хафмана в JPEG.

В комп’ютерній техніці набори символів маже завжди представляють методами кодування з фіксованою довжиною коду (fixed-length encoding method)(напр. ASCII чи EBCDIC), які не враховують частоту їх використання в роботі. Це дуже ефективно для досягнення найбільшої швидкості обчислень. Але при стисненні зображень де розмір даних відіграє велику роль, доцільно використовувати коди змінної довжини. За таким методом кодується, наприклад, азбука морзе. (* = «Є»;- = «Т»).

Найвідомішим шрифтом генерування кодів змінної довжини, на основі частоти їх використання є метод кодування Хафмана (запропонований в 1952р.)

Процедура формування кодів Хафмана вимагає створення двійкового дерева, що вміщує символи. Символ, що зустрічаються рідко знаходяться далі від кореня. Створюється так-званий пул (pool), який може вміщувати значення та вузли дерева. Початково цей пул має всі значення і не вміщує вузлів.

Алгоритм (процедура) кодування Хафмана.

1.Знайти два значення чи вузли дерева з найменшою частотою появи і видалити їх з пулу.

2. Створити новий вузол дерева і зробити елементи із попереднього кроку його гілками.

3. Присвоїти новому вузлу дерева частоту, що дорівнює сумі частот гілок, що відходять від

нього.

4.Добавити створений вузол в пул.

Ця процедура повторюється до тих пір, поки пул не буде складатись з одного вузла дерева і в ньому не буде жодного вузла дерева і в ньому не буде жодного вузла символу. Після цього кожному вузлу дерева призначається значення 0 одній його гілці, та значення 1 другій. Код Хафмана визначається проходом по шляху від кореня дерева до даного значення і додаванням у загальний код, коду кожної гілки.

Множина кодових значень утворює так-звану таблицю Хафмана.

Закодуємо поліндром(рядок, що читається однаково за обома напрямками):

A MAN A PLAN A CANAL PANAMA.

Початковій пул:

A C L M N P <SPACE>.

10 1 2 2 4 2 6 1

1. Два значення з найменшою появою у тексті (=1)-символи «С» та «.». Використовуємо ці символи для створення вузла дерева. Призначаємо цьому вузлу значення частоти, що дорівнює частоті гілок, що відходять від вузла. Маємо пул з вузлом дерева:

A L M N P <SPACE>

10 2 2 4 2 6

С.

1 1

2. Чотири елементи, що відображені в пулі, мають нижчу частоту, що = 2. Беремо «P» і вузол дерева, з’єднуємо їх між собою, щоб створити новий вузол дерева із сумарною частотою, що = 4.

A L M N <SPACE>

10 2 2 4 6

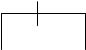
4

Р2

С.

1 1

3. Тепер із залишених символів найменша частота зустрічається у букв L та M. Оскільки всім доступним гілкам дерева призначені більші частоти, необхідно створити новий вузол, не з’єднаний з деревом:

A N <SPACE>

10 4 4 6 4

L M Р

2 2 2 С.

1 1

4. Тепер є два вузли дерева та буква «N», що зв’язані з найменшою частотою, що = 4. Ми обираємо букву «N» і приєднуємо її до дерева:

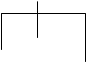A <SPACE>

10 4 6 N 4

4 2

L M Р

2 2 2 С.

1 1

5. Із залишених елементів:

A

10 10 8

<SPACE> 4 N 4

6 4 2

L M Р

2 2 2 С.

1 1

6. Тепер залишились 2 вузла дерева та буква «А». Ми довільно вирішуємо з’єднати два вузли дерева, а не букву з одним із цих вузлів:

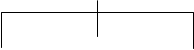A 18

10 10 8

<SPACE> 4 N 4

6 4 2

L M Р

2 2 2 С.

1 1

Дата добавления: 2014-12-23