Frequencies statistics - описанельные статистики

FREQUENCIES NTILES, percentiles - процентили

Подкоманда NTILES задает печать n-тилей - значений переменной, делящих распределение на заданное число групп с равным числом объектов. Следующая команда выдает квинтили по доходу:

FREQUENCIES /VARIABLES=V14 /NTILES=5.

Подкоманда PERCENTILES печатает процентили (процентиль - это квантиль, рассчитанная по доле, указанной в процентах). Процентили являются значениями переменной, отделяющими указанную в процентах долю совокупности объектов. Процентили удобно использовать, если нам нужно разбить значения переменной на интервалы, которые содержали бы определенного размера группы объектов (анкет). Пример: найдем значения дохода, отделяющие 10% выборки, 50% (медиану) и 90%.

FREQUENCIES /VARIABLES= V14 /PERCENTILES 10 50 90.

Подкоманда позволяет получить одномерные описательные статистики.

FREQUENCIES V1 V2 V4 /STATISTICS DEFAULT.

Ключевые слова:

MEAN - среднее;

SEMEAN - стандартная ошибка среднего;

MEDIAN - медиана(процентиль с 50%)

MODE - мода(наиболее частое значение)

STDDEV - стандартное отклонение;

VARIANCE - дисперсия;

KURTOSIS - эксцесс (пикообразность);

SEKURT - стандартная ошибка эксцесса

SKEWNESS - коэффициент асимметрии (скошенность);

SESKEW - стандартная ошибка коэффициента асимметрии;

RANGE - разброс = (MAX - MIN);

MINIMUM - минимум;

MAXIMUM - максимум;

SUM - сумма всех значений переменной;

ALL - все статистики.

DEFAULTS - по умолчанию МEAN, STDDEV, MIN, MAX.

Для расчета параметра SEMEAN (стандартной ошибки среднего для выборки x₁, x₂,…, x_n) вычисляются следующие статистики:

MEAN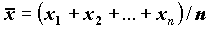

VARIANCE: - оценка дисперсии;

SEMEAN - оценка стандартной ошибки среднего.

Стандартную ошибку можно использовать для оценки доверительного интервала среднего. Напомним, что доверительным интервалом параметра называется интервал со случайными границами, накрывающий значение параметра с заданной (доверительной) вероятностью. В частности, приближенными оценками границ 95% двустороннего доверительного интервала являются значения 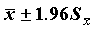(истинное значение среднего с вероятностью 0.95 находится в этих пределах).

Если распределение нормально, то в пределах должно находиться примерно 68% наблюдений совокупности.

Скошенность определяется расчетом третьего момента по следующей формуле:

SKEWNESS: - коэффициент асимметрии.

Если полученная величина < 0, то распределение растянуто влево, если > 0, то вправо.

Пикообразность определяется значением четвертого момента:

KURTOSIS: - эксцесс.

Таблица 3.2. Статистики по переменной V14 - "Душевой доход", выданные командой FREQUENCIES

N	Valid
	Missing
Mean		229.11
Std. Error of Mean		5.83
Median
Mode
Std. Deviation		151.342
Variance		22904.531
Skewness		3.035
Std. Error of Skewness		0.094
Kurtosis		15.080
Std. Error of Kurtosis		0.188
Range
Minimum
Maximum
Sum
Percentiles

Чем больше четвертый момент, тем больше пикообразность распределения; нулевое значение KURTOSIS означает, что пикообразность распределения совпадает с пикообразностью нормального распределения. Существенность отклонений статистик от теоретических можно проверить, используя стандартные ошибки этих статистик (в основе лежит факт, что отношение статистики к ее стандартной ошибке имеет распределение, близкое к нормальному).

Перечисленные статистики играют в анализе данных особую роль - они позволяют провести первый этап статистических исследований выборки, проверить нормальность ее распределения. Ниже приведен пример описательных статистик, полученных для переменной "Среднемесячный душевой доход в семье", построенной по ответам на 14-й вопрос анкеты "Курильские острова" командой

FREQUENCIES VARIABLES=V14 /NTILES=4 /PERCENTILES= 10 90

/STATISTICS=STDDEV VARIANCE RANGE MINIMUM MAXIMUM SEMEAN MEAN MEDIAN MODE SUM SKEWNESS SESKEW KURTOSIS SEKURT.

которая вычисляет, также, n -тили и процентили.

Анализируя полученные данные (таблица 3.2), видим, что доход в семьях меняется в диапазоне от 21 рубля до 1500 рублей (разброс равен 1479). При этом средний доход составил около 230 рублей. Приближенными границами пятипроцентного доверительного интервала для истинного среднего будут значения: 229.11± 1.96*5.83, где 1.96 - критическое значение нормального распределения для p=0.05/2=0.025. Скошенность skewness=3.035 Пикообразность kurtosis=15.080 и пикообразность kurtosis=15.080 значительно больше нуля (их стандартные ошибки, 0.094 и 0.188, свидетельствуют о статистической значимости такого отличия).

Результатом задания процентилей и n-тилей являются выданные в таблице процентили (у 10% выборки доход меньше 100 руб., у 90% - меньше 400; имеются также 25%, 50%, 75% процентили).

Дата добавления: 2014-12-27