STATISTICS - исследование связи неколичественных перемееных

В предыдущем разделе изучалась связь значений переменных. Для получения ответа о связи переменных в целом используется подкоманда STATISTICS с параметрами, указывающими на статистику или коэффициент для исследования связи переменных. Вот некоторые из этих параметров:

CHISQ - позволяет оценить связь с помощью критерия Xи-квадрат; кроме коэффициента Xи-квадрат при задании этого ключевого слова выдается отношение правдоподобия (Likelihood Ratio). А также статистика для проверки линейной связи. Последняя статистика редко используется, в связи с чем не рассматривается в данных методических рекомендациях.

PHI - коэффициент PHI-Пирсона; вместе с этим коэффициентом выдается коэффициент V-Крамера;

CC - коэффициент контингенции;

BTAU - Тау-В Кендалла для ранговых переменных;

CTAU - Тау-С Стюарта для ранговых переменных;

ALL - указанные статистики и еще около десятка различных статистик.

Как можно охарактеризовать в целом связь НЕКОЛИЧЕСТВЕННЫХ переменных? Для характеристики связи номинальных переменных наиболее часто используется критерий Xи-квадрат (CHISQ), основанный на вычислении статистики

CHISQ= .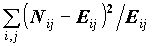

Эта статистка показывает расстояние эмпирически полученной таблицы сопряженности от ожидаемой теоретически: расстояние между значениями выборочной таблицы N_ij и ожидаемой в условиях независимости таблицы E_ij. Само по себе значение статистики ни о чем не говорит, важно знать вероятность получения расстояния CHISQ, большего, чем наблюдаемое на случайной выборке. Эта вероятность называется наблюдаемой значимостью и обозначается словом SIGNIFICANCE (возможны сокращения - Sig., P -значения).

CHISQ в условиях независимости и при достаточном числе наблюдений имеет распределение, близкое к распределению Xи-квадрат с (r-1)(c-1) степенями свободы, где r - число строк в таблице, с число столбцов (CHISQ_{теор.» c} ²((r-1)(c-1))). Существует эмпирическое правило, по которому считается, что CHISQ достаточно точно аппроксимируется теоретическим распределением c ²((r-1)(c-1)), если среди ожидаемых частот E_ij не более 20% меньше 5 и нет E_ij, меньших 1. Поэтому рекомендуется использовать критерий хи-квадрат в CROSSTABS для переменных с небольшим числом значений, что достигается перекодировкой переменных. В выдаче присутствует информация о числе клеток, где это соотношение не выполняется. Пакет выдает выборочное значение CHISQ и его значимость. Вместе с критерием Xи-квадрат выдается также логарифм отношения правдоподобия LI:

,

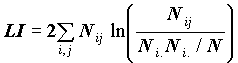имеющее асимптотически то же распределение, но более устойчивое к объему выборки. Поэтому при оценке связи пары признаков мы рекомендуем пользоваться отношением правдоподобия. Для всех критериев выдается значимость:

SIGNIFICANCE - вероятность случайно получить большее значение, чем выборочное. Таким образом, для CHISQ наблюдаемая значимость (SIG) равна P{CHISQ_теор.>CHISQ_{выбороч.}} и, аналогично, для отношения правдоподобия LI наблюдаемая значимость (SIG) равна P{LI_теор.>LI_{выбороч.}}. Пример задания для исследования связи ответа на вопрос о необходимости иностранной помощи(v1) и полом (v8):

CROSSTABS v8 by v1 /cells count row col asresid /STATISTICS=CHISQ.

Таблица 3.6. Тесты ХИ-квадрат

	Value	df	Asymp. Sig. (2-sided)
Pearson Chi-Square	10.517		.015
Likelihood Ratio	10.708		.013
Linear-by-Linear Association	.156		.693
N of Valid Cases

a 0 cells (.0%) have expected count less than 5. The minimum expected count is 22.25.

В приведенном примере наблюдаемая значимость CHISQ составила около 1.5% (см. Asymp. Sig. (2-sided)), значимость LI примерно 1.3%. С такой вероятностью случайно в условиях независимости можно получить большие значения соответствующих статистик, поэтому, в соответствии с 5% уровнем значимости, переменные v8 и v1 следует считать связанными (1.3%<5%). Таким образом, мужчины и женщины имеют разные мнения в вопросе об иностранной помощи.

Если теперь взглянуть на Z -статистики, можно увидеть, в клетке "мужчины" - "помощь нужна" эта статистика равна 2.9, и о помощи говорят вдвое больше мужчин, чем женщин. Мы не будем приводить здесь эту таблицу, а покажем лишь столбиковую диаграмму на рис.3.4, полученную командой

ROSSTABS v8 by v4 /cells count row col asresid/BARCHART.

Дата добавления: 2014-12-27