Z статистика отклонения средних

При анализе средних в таблицах для неальтернативных признаков, каждая ячейка рассматривается по отдельности и среднее в группе, соответствующей ячейке, сравнивается со средними в ее дополнении.

Обозначим A совокупность объектов, соответствующую i -тому ответу вертикального и j -му ответу горизонтального вопросов, B - ее дополнение. Число объектов в группе A равно . Группа объектов B может иметь разное содержание в зависимости от того, с чем мы хотим сравнить среднее в этой группе: 1) со средним по всей совокупности, тогда B - дополнение A до всей совокупности и содержит 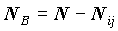объектов; 2) с итоговым средним по строке, тогда B - дополнение A до i -той группы по вертикальному вопросу, а ; 3) с итоговым средним по столбцу, тогда B - дополнение A до j -той группы по горизонтальному вопросу, а .

Для проверки значимости различия средних в группах A и B в предположении теоретического нормального распределения, при несовпадении дисперсии в группах используется статистика 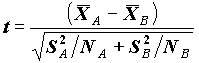, имеющая распределение Стьюдента с числом степеней свободы, зависящем от оценок дисперсии , 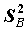и от объемов групп.

Статистика t характеризует отклонение среднего в группе A от среднего в группе B, но, поскольку , можно утверждать, что эта же статистика характеризует отклонение от итогового среднего 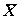. Вероятность среднего в ячейке быть меньше итогового среднего равна в условиях гипотезы независимости . Для вычисления статистики Z используется формула Z=Ф^-1(P{t<t_выб}), где Ф^-1 - обратная функция распределения нормального (N(0,1)) закона. Ясно, что Z -статистика в условиях равенства средних и нормальности распределений имеет стандартное нормальное распределение.

Как выяснить надежность результата?

В соответствии с общепринятым использованием 5%-го уровня значимости, мы можем заявить, что величина стандартизованного смещения Z, превышающая 1.96, свидетельствует о существенности связи (вероятность в условиях независимости получить большее смещение равна 5%, см. выделенные клетки со значимыми смещениями в табл.2). Однако это утверждение о значимости верно только для отдельно взятой клетки таблицы, как мы ранее показали, вероятность того, что в этой таблице из 100 независимых клеток имеется хотя бы одна "значимая" статистика, равна. Это - результат множественных сравнений статистик.

Чтобы снизить вероятность принятия случайных отклонений за закономерные, нужно использовать более жесткий критерий, хотя, конечно, и обычное применение Z -статистик позволяет избежать очевидных глупостей.

К сожалению, таблицу с Z -статистиками, подобную таблице 2, обычными средствами статистических пакетов получить сложно - в них нет средств анализа значимости по неальтернативным вопросам.

Дата добавления: 2014-12-27