Емтихан билеті №2, 20, 21, 26, 27 2 страница

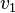және 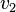жылдамдықпен бір-біріне қарама-қарсы бағытта қозғалып келе жатқан массалары 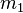және 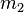екі шардың өзара әрекеттесуін қарастырайық. Өзара әрекеттесу күштері қандай болса да, олар Ньютонның үшінші заңы бойынша байланысады: 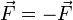немесе

мұндағы — өзара әрекеттесу уақыт аралығы, 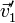және 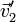— шарлардың өзара әрекеттесуінен кейінгі жылдамдықтары.

Шарлардың өзара әрекеттескенге дейінгі импульстерін теңдіктің бір жағына, өзара әрекеттескеннен кейінгі импульстерін тендіктің екінші жағына шығарсақ, онда 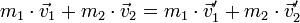болады.

Теңдеудің сол жағында денелердің өзара әрекеттескенге дейінгі, оң жағында өзара әрекеттескеннен кейінгі импульстерінің қосындысы берілген және олар өзара тең. Әрбір дененің импульсі өзгергенімен, олардың импульстерінің қосындысы өзгеріссіз қалды. Сонымен, тұйық жүйедегі өзара әрекеттесетін денелер импульстерінің қосындысы өзгермейді (сақталады):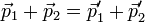

Бұл — импульстің сақталу заңы деп аталатын табиғаттың негізгі заңдарының бірі. Егер біз қарастырған мысалдағыдай екі дене ғана болмай, бірнеше дене әрекеттессе де, бұл қорытынды кезкелген тұйық жүйе үшін дұрыс болып табылады. Бұл заңның дұрыстығын адамзат тәжірибесінің өзі айқын дәлелдеп беріп отыр.

Әрине, барлық нақты жүйелер тұйық болып табылмайды. Алайда импульстің сакталу заңын көп жағдайда қолдануға болады.

Қуат. Механизмнің уақыт бірлігінде істейтін жұмысын қуат деп атайды.

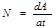
мұндағы dA – жұмыс, dt – уақыт, яғни қуат – жұмыстың уақыт бойынша алынған туындысы. Егер қозғалтқыштың (двигательдің) жұмыс істеуі кезінде қуаты тұрақты болса, оның қозғалысы бір қалыпты болады, ендеше қуат: күш векторының жылдамдық векторына скалярлық көбейтіндісін береді

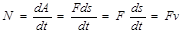
Қуаттың өлшем бірлігі - Ватт (Вт), 1Вт – 1с –та 1 Дж жұмыстың жасалуы, 1Вт=1Дж/с.

Энергия.

Табиғатта жұмыс істеу салдарынан материя қозғалысының формасы бір түрден екінші түрге өзгеріп отырады. Осы өзгеріс кезінде жұмыс жасалынады, бұл жұмыс - энергия деп аталады. Сондықтан, неғұрлым жұмыс көбірек жасалынса, соғұрлым энергия көп болады.

Дененің жұмыс істеу қабілеттілігінің сандық мөлшерін энергия деп атайды.

Энергия жұмыспен тығыз байланысты болғандықтан, жұмыс қандай өлшем бірлікпен өлшенсе, энергия да сондай өлшем бірлікпен өлшенеді.

Кинетикалық энергия.

Материалдық нүктеге түсірілген күштің жасаған жұмысы дененің жылдамдығының өзгеруіне байланысты. Бұл байланыс материалдық нүктенің кинетикалық энергиясы деп аталады.

Егер дене инерция күшінің нәтижесінде ds –ке орын ауыстырса, істелген жұмыс

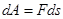, бұдан:

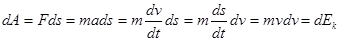
яғни, v жылдамдықпен қозғалатын массасы m дененің кинетикалық энергиясы:

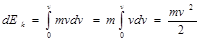
Сонымен, кинетикалық энергия дененің тек массасы мен жылдамдығына тәуелді. Сондықтан, ол 1) жүйенің күй функциясы болып табылады; 2) барлық уақытта оң;

3) әртүрлі инерциалды санақ жүйесінде бірдей емес.

Потенциалдық энергия.

Потенциалдық энергия - денелердің өзара орналасуын және араларындағы әсерлесу күшін сипаттайтын жүйенің механикалық энергиясы. Потенциалдық энергия денелердің немесе олардың бөлшектерінің өзараорналасуы кезіндегіжұмыс қорымен өлшенеді. Мысалы, материалдық нүкте ауырлық күшінің біртекті өрісінде қозғалғанда, яғни бір денені бірдеңгейден екінші деңгейге көтергенде істелетін жұмысты есептеу арқылы потенциалдық энергияны табуға болады. Массас ы m дене Жербетінен h биіктіккекөтерілсін, сонда оның потенциалдық энергиясы жасалынған жұмысқа тең: 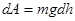немесе 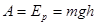Ендеше: 1) массасы m дененің h биіктікке көтерілген кездегі потенциалдық энергиясы:

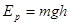
2) х – ұзындыққа созылған серіппенің потенциалдық энергиясы:

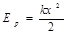
2. Ток көздердің ЭҚК. Толық тізбек үшін Ом заңы. Тармақталған тізбек үшін Кирхгоф ережелері, Ом жэне Джоуль-Ленц заңдарының дифференциалдық түрі.

Тұрақты электр тоғы. Тұрақты электр тогы, оның сипаттамалары және пайда болу шарттары. Электр қозғаушы күші, кернеу. Тізбектің біркелкі және әркелкі бөліктері үшін Ом заңы. Дифференциал түріндегі Ом және Джоуль-Ленц заңы. Кирхгоф ережелері. Газдардағы ток. Термоэлектрондық эмиссия

Тұрақты электр тогы. Зарядталған бөлшектердің реттелген қозғалысын - электр тогы дейміз. Электр тогы ток күші деп аталатын шамамен сипатталады. Ток күші уақыт бірлігі ішінде берілген өткізгіштің көлденең қимасынан өтетін зарядтар шамасы: 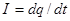. Бұл өрнек токтың лездік мәнін сипаттайды. Егер токтың күші мен бағыты уақыт өтуіне сәйкес өзгермейтін болса, онда мұндай ток тұрақты ток деп аталады: ;

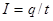Мұндағы: q - өкізгіштің көлденең қимасы арқылы t уақыт ішінде өтетін электр заряды. Тоқ күшінің өлщемі - 1 Ампер. Электр тогы өзі өткен бет бойынша біркелкі таралмауы да мүмкін. Электр тогы сан жағынан ток тығыздығы деген шамамен сипатталады. Сонымен ток тығыздығы деп өткізгіштің бірлік көлденең қимасынан өтетін ток күшін айтамыз: 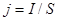. Егер де ток өткізгіштің көлденең қимасынан біркелкі өтпесе, онда ток тығыздығы: .

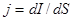Егер dt уақыт ішінде өткізгіштің көлденең қимасы арқылы заряд тасымалданса 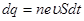(мұндағы n, e, 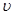- концентрация, заряд және зарядтың реттелген қозғалысының жылдамдығы), онда ток күші .

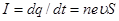Ал, өткізгіштегі ток тығыздығы мынаған тең болады: .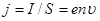

Тоқ тығыздығы - векторлық шама. Өлшем бірлігі: .

Электр тогы тұрақты болу үшін өткізгіштің ұштарындағы потенциалдар айырымы (немесе кернеуі) тұрақты болу керек. Өткізгіштің тұрақты кернеуін болдыру үшін белгілі бір энергия қоры қажет. Осындай тұрақты кернеуді әдетте ток көздері немесе кернеу көздері деп атайды.

Кез келген ток көзінің ішкі кедергісі r болады. Ток көзінің екі полюсі болады, оның жоғары потенциалы бар жағы - оң, төменгі потенциалы бар жағы - теріс деп аталады. Осы полюстердің арасында потенциалдар айырымы болады. Сонда ток көзінің полюстеріндегі кернеу: 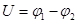. Әдетте, электр өрісі өткізгіште потенциалдың кему жағына қарай бағытталған токты туғызады. Электр кернеуінің бағыты да осы потенциалдың кему жағына бағытталады.

Егер ток көзінің ішінде электрлік кернеуліктен басқа ешқандай әсер болмаса, онда зарядтар қозғалысы оң полюстен теріс полюске бағытталып, ішкі кедергісі арқылы ток жүрер еді де, потенциалдары теңескеннен кейін токтың жүруі тоқтар еді. Ал, шын мәнінде ток көзі сыртқы тізбекке қосылмағандықтан, оның кернеуі ұзақ сақталады, сөйтіп онда ешқандай ток болмайды. Өйткені, ток көзінде электростатикалық күштерден басқа күштер, яғни бөгде күштер деп аталатын күштер бар. Зарядтарды тасымалдау жұмысын жасайтын бөгде күштерді, әдетте электр қозғаушы күштер (э.қ.к.) деп атайды.

Сонымен, ток көздерін э.қ.к. көздері дейді де, оны 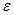әрпімен белгілейді: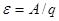

Э.қ.к. - нің өлшемі потенциал өлшеміндей, яғни 1 Кл зарядты тасымалдау үшін істелетін жұмыс 1Дж болатын э.қ.к. өлшеміне 1В алынады: .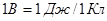

Ток потенциалдың кему жағына қарай бағытталған. Электр күштері арқылы орын ауыстырған зарядтың жұмысы: , .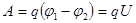

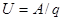Ұзындығы l өткізгіштің ұштарындағы потенциалдар айырымы немесе кернеуі: 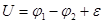. Мұндағы, 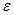ток көзінің э.қ.к. - і.

Тұйық тізбектегі зарядқа әсер ететін бөгде күш: 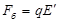. Мұндағы 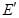бөгде күштің өріс кернеулігі.

Тұйық тізбектегі зарядқа әсер ететін бөгде күштің жұмысы: .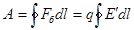

Зарядқа тағы да электростатикалық өріс күші әсер етеді: .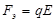

Демек, тізбектің әрбір нүктесіндегі зарядқа әсер ететін қорытқы күш:

.

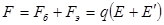Ал, осы күштің тізбектің l бөлігіндегі жұмысы:

^.

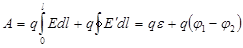Тұйық тізбек үшін электростатикалық күштің жұмысы нөлге тең, сондықтан: ^.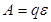

Ом заңдары. Өткізгіштің кедергісі. Омның тағайындаған заңы бойынша біртекті металл өткізгіштің бойымен ағатын ток күші осы өткізгішке түсірілген U кернеуге пропорционал болады: 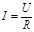. Бұл өрнек тізбек бөлігі үшін Ом заңы деп аталады.

Тұйық тізбек үшін Ом заңы былай тұжырымдалады: тұйық тізбектегі ток күші э.қ.к.- і шамасына тура пропорционал да, тізбектің сыртқы және ішкі кедергілерінің қосындысына кері проорционал болады. Яғни, .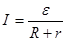

Бөгде күштер әсер етейтін өткізгіш біртекті өткізгіш деп аталады. R шамасы өткізгіштің электрлік кедергісі деп аталады. Өлшем бірлігі: Ом. Өткізгіштің кедергісі өткізгіштің материалына, өлшеміне және формасына байланысты.

Біртекті цилиндр тәрізді өткізгіш үшін: 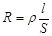. Мұндағы: l - өткізгіштің ұзындығы, S – оның көлденең қимасының ауданы, 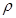өткізгіштің меншікті электрлік кедергісі.

Ом заңының дифференциалды түрі мынадай: .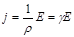

Мұндағы: 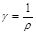- материалдың өткізгіштігі деп аталады.

Өткізгіштерді тізбекке қосудың екі түрі бар: егер өткізгіштерді тізбектей қоссақ, онда олардың толық кедергісі 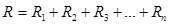болады. Өткізгіштерді параллель қоссақ, онда олардың толық кедергісі .

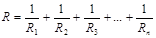Тоқтың қуаты. Джоуль - Ленц заңы.

Электр күштерінің жұмысы: .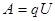

Өткізгіштің қимасынан dt уақыт ішінде q заряд ағып өтеді десек, онда q=It.

Сонда, электр тогының жұмысы: dA=IUdt. Ал, тұрақты ток үшін: A=IUt.

Тоқтың қуаты: .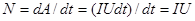

Қуаттың өлшем бірлігі: Ватт. Сонда: 1 Вт= 1А·В болады.

Егер ток қозғалмайтын металл өткізгіш арқылы жүрсе, онда біршама жылу бөлініп шығады, осы кезде ток жұмысы энергияның сақталу заңына байланысты жылуға айналады: dA=dQ. Cөйтіп, бұл жылу мөлшерін A=IUt өрнегін ескере отырып былай жазуға болады: 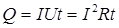. Бұл өрнек Джоуль – Ленц заңы деп аталады.

Джоуль – Ленц заңы былай тұжырымдалады: өткізгіштен бөлініп шығатын жылу мөлшері уақытқа, өткізгіштің кедергісіне және ток күшінің квадратына пропорционал болады. Жылу мөлшері де жұмысқа сәйкес Дж -мен өлшенеді.

Джоуль – Ленц заңының дифференциалды түрі: .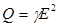

Тармақталған тізбек үшін Кирхгоф ережелері:

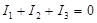. Жалпы түрде: . Бұл өрнек Кирхгофтың бірінші ережесі деп аталады. Мұны былайша түсіндіруге болады: егер түйіндегі токтардың алгебралық қосындысы нөлден өзгеше болса, түйінде зарядтар көбейіп не азайып кетер еді де, бұл өз кезегінде түйіндегі потенциалдың және тізбектен ағатын токтың өзгеруіне әкеп соғар еді. Кирхгофтың екінші ережесін жалпы түрде энергияның сақталу заңына сүйеніп, тармақталған тізбек үшін Ом заңын қорытындылау арқылы түсіндіруге болады. -кез келген тұйық контур үшін э.қ.к.-нің алгебралық қосындысы ток күшінің кедергіге көбейтіндісінің алгебралық қосындысына тең. Бұл өрнек Кирхгофтың екінші ережесі деп аталады.

3. Кернеулігі 2000 В/м болатын біртекті электр өрісі шамасы 5×10^–6 Кл зарядқа қандай күшпен әсер етеді:

E 2000В/м

q 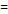5*10^-6Кл

F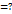

E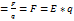

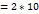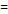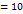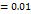E ³*5*10^-6 10*10^{-3 -2} Н

ЕМТИХАН БИЛЕТІ №5

1. Идеал газ молекулаларын жылдамдықтары бойынша жіктеудің максвелл заңы. Барометрлік формула.

Молекулалық-кинетикалық теорияның негізгі заңын қорытқан кезде молекулалар әртүрлі жылдамдықпен қозғалады дедік. Көптеген соқтығысулар нәтижесінде әр молекуланың жылдамдығы модулі және бағыты бойынша өзгереді. Бірақ молекулалардың хаосты қозғалуының нәтижесінде барлық қозғалыс бағыттары ықтимал, яғни орташа есеппен кез-келген бағытта қозғалатын молекулалар саны бірдей.

Молекулалық-кинетикалық теория бойынша молекулалар соқтығысқанда жылдамдық қанша өзгергенімен газдағы массасы m₀ молекуланың тепе-теңдік қалыпта тұрақты температурадағы Т= const орташа квадраттық жылдамдығы 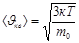тең. Мұны былай түсіндіруге болады: Т= const болғанда тепе-теңдік күйдегі газда уақыт уақыт бойынша өзгермейтін молекулалардың жылдамдық бойынша таралуы, яғни стационар таралуы орын алады. Ол белгілі бір статистикалық заңға бағынады, теория жүзінде ол заңды қорытып шығарған Дж. Максвелл.

Молекулалардың жылдамдық бойынша таралу заңын қорытып шығарғанда Максвелл газ өте көп молекулалардан тұрады, молекулалар бірдей температурада тәртіпсіз жылулық қозғалыста болады және газға күш өрістері әсер етпейді деп алды.

Максвелл заңы 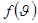функциясымен сипатталады, ол функция молекулалардың жылдамдық бойынша таралу функциясы деп аталады.

Егер молекулалардың жылдамдық диапазонын 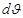-ға тең кіші интервалдарға бөлсек,онда жылдамдықтың әрбір интервалына 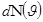молекулалар саны келеді, 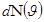молекулалардың жылдамдығы осы интервалда жатады.

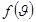функциясы жылдамдықтары 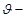дан 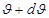интервалында жатқан молекулалардың салыстырмалы санын анықтайды: 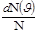, яғни

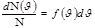бұдан .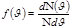

Ықтималдылық теориясының әдістерін пайдалана отырып, Максвелл 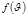функциясын – идеал газ молекулаларының жылдамдық бойынша таралу заңын тапты: 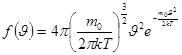(1)

Формуладан көргендей 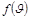функциясы газдың массасына және температураға Т тәуелді. (түсініксіз 9-ға ұқсайтын әріп ол – V)

Дата добавления: 2014-12-27