Построение двухмерных графиков

Работа с графикой

Работа с текстом

Текстовые фрагменты представляют собой куски текста, которые пользователь хотел бы видеть в своем документе. Это могут быть пояснения, ссылки, комментарии и т.д. Они вставляются при помощи пункта меню Вставка – Текстовый регион.

Вы можете отформатировать текст: поменять шрифт, его размер, начертание, выравнивание и т.д. Для этого нужно его выделить и выбрать соответствующие параметры на панели шрифтов или в меню Форматирование– Текст.

При решении многих задач, где производится исследование функции, часто возникает необходимость в построении ее графика, где наглядно будет отражено поведение функции на определенном промежутке.

В системе MathCAD существует возможность построения различных видов графиков: в декартовой и полярной системе координат, трехмерных графиков, поверхностей тел вращения, многогранников, пространственных кривых, графиков векторного поля. Мы рассмотрим приемы построения некоторых из них.

Для построения двухмерного графика функции необходимо:

· задать диапазон значений аргумента;

· задать функцию;

· установить курсор в то место, где должен быть построен график, на математической панели выбрать кнопку Graph (график) и в открывшейся панели кнопку X-Y Plot (двухмерный график);

· в появившемся шаблоне двухмерного графика, представляющем собой пустой прямоугольник с метками данных, в центральную метку данных по оси абсцисс (ось X) ввести имя переменной, а на месте центральной метки данных по оси ординат (ось Y) ввести имя функции (рис. 2.1);\

Имя переменной

Имя функции

Рис. 2.1. Шаблон двухмерного графика

щелкнуть мышью вне шаблона графика — график функции будет построен.

Диапазон изменения аргумента состоит из 3-х значений: начальное, второе и конечное.

Пусть необходимо построить график функции на интервале [-2,2] с шагом 0.2. Значения переменной t задаются в виде диапазона следующим образом:

t:= –2, –1.8.. 2,

где: –2 — начальное значение диапазона;

–1.8 (–2 + 0.2) — второе значение диапазона (начальное значение плюс шаг);

2 — конечное значение диапазона.

!

Внимание. Многоточие вводится нажатием точки с запятой в английской раскладке клавиатуры.

Пример. Построение графика функции y = x ² на интервале [–5,5] с шагом 0.5 (рис. 2.2).

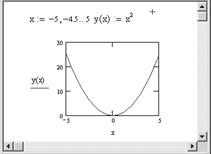
Рис. 2.2. Построение графика функции y = x ²

При построении графиков необходимо учитывать следующее:

° Если диапазон значений аргумента не задан, то по умолчанию график строится в диапазоне [–10,10].

° Если в одном шаблоне необходимо разместить несколько графиков, то имена функций указываются через запятую.

° Если две функции имеют различные аргументы, например f1(x) и f2(y), то на оси ординат (Y) через запятую указываются имена функций, а по оси абсцисс (X) — имена обеих переменных тоже через запятую.

° Крайние метки данных на шаблоне графика служат для указания предельных значений абсцисс и ординат, т.е. они задают масштаб графика. Если оставить эти метки незаполненными, то масштаб будет установлен автоматически. Автоматический масштаб не всегда отражает график в нужном виде, поэтому предельные значения абсцисс и ординат приходится редактировать, изменяя вручную.

Примечание. Если после построения график не принимает нужный вид, можно:

· уменьшить шаг.

· изменить интервал построения графика.

· уменьшить на графике предельные значения абсцисс и ординат.

Пример. Построение окружности с центром в точке (2,3) и радиусом R = 6.

Уравнение окружности с центром в точке с координатами (x ₀, y ₀) и радиусом R записывается в виде:

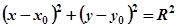
Выразим из этого уравнения y:

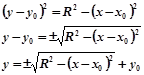
Таким образом, для построения окружности необходимо задать две функции: верхнюю и нижнюю полуокружности. Диапазон значений аргумента вычисляется следующим образом:

- начальное значение диапазона = x ₀ – R;

- конечное значение диапазона = x ₀ + R;

- шаг лучше взять равным 0.1 (рис. 2.3.).

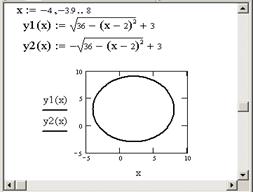
Рис. 2.3. Построение окружности

Дата добавления: 2014-12-27