Решение уравнений с помощью функции Polyroots(v)

Решение уравнений с помощью функции root(f(x),x)

Способы решения уравнений в MathCAD

Форматирование трехмерных графиков

Для форматирования графика необходимо дважды щелкнуть по области построения — появится окно форматирования с несколькими вкладками: Appearance, General, Axes, Lighting, Title, Backplanes, Special, Advanced, Quick Plot Data.

Назначение вкладки Quick Plot Data было рассмотрено выше.

Вкладка Appearance позволяет менять внешний вид графика. Поле Fill Options позволяет изменить параметры заливки, поле Line Option — параметры линий, Point Options — параметры точек.

Во вкладке General ( общие) в группе View можно выбрать углы поворота изображенной поверхности вокруг всех трех осей; в группе Display as можно поменять тип графика.

Во вкладке Lighting (освещение) можно управлять освещением, установив флажок Enable Lighting (включить освещение) и переключатель On (включить). Одна из 6-ти возможных схем освещения выбирается в списке Lighting scheme (схема освещения).

В данном разделе мы узнаем, каким образом в системе MathCAD решаются простейшие уравнения вида F(x) = 0. Решить уравнение аналитически — значит найти все его корни, т.е. такие числа, при подстановке которых в исходное уравнение получим верное равенство. Решить уравнение графически — значит найти точки пересечения графика функции с осью ОХ.

Для решений уравнения с одним неизвестным вида F(x) = 0 существует специальная функция

root(f(x),x),

где f (x) — выражение, равное нулю;

х — аргумент.

Эта функция возвращает с заданной точностью значение переменной, при котором выражение f (x) равно 0.

!

Внимание. Если правая часть уравнения ¹0, то необходимо привести его к нормальному виду (перенести все в левую часть).

Перед использованием функции root необходимо задать аргументу х начальное приближение. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.

!

Внимание. Перед решением желательно построить график функции, чтобы проверить, есть ли корни (пересекает ли график ось Ох), и если есть, то сколько. Начальное приближение можно выбрать по графику поближе к точке пересечения.

Пример. Решение уравнения с помощью функции root представлено на рисунке 3.1. Перед тем как приступить к решению в системе MathCAD, в уравнении все перенесем в левую часть. Уравнение примет вид: .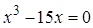

Рис. 3.1. Решение уравнения при помощи функции root

Для одновременного нахождения всех корней полинома используют функцию Polyroots(v), где v — вектор коэффициентов полинома, начиная со свободного члена. Нулевые коэффициенты опускать нельзя.В отличие от функции root функция Polyroots не требует начального приближения.

Пример. Решение уравнения с помощью функции polyroots представлено на рисунке 3.2.

Рис. 3.2. Решение уравнения с помощью функции polyroots

Дата добавления: 2014-12-27