Организация циклов. IF a+b>=c AND b^2>a THEN ?

INPUT a,b,c

IF a+b>=c AND b^2>a THEN? “Верно” ELSE? “Неверно”

Аргумент	Функция НЕ		Первый аргумент	Второй аргумент	Функция И	Функция ИЛИ
Ложь	Истина		Ложь	Ложь	Ложь	Ложь
Истина	Ложь		Ложь	Истина	Ложь	Истина
			Истина	Ложь	Ложь	Истина
		Истина	Истина	Истина	Истина
Таблица 2.3.2			Таблица	2.3.3

Другой пример. Для произвольных чисел А, В, С выяснить, правда ли что первое число самое большое, а последнее – самое маленькое.

IF a>b AND a>c AND c<a AND c<b

THEN? “Верно” ELSE? “Неверно”

Еще. Правда ли, что среди чисел А, В, С имеется ровно одна единица.

IF (a=1 AND b<>1 AND c<>1) OR

(a<>1 AND b=1 AND c<>1) OR

(a<>1 AND b<>1 AND c=1)

THEN? “Верно” ELSE? “Неверно”

Здесь скобки введены только для наглядности поскольку операция AND все равно выполняется прежде операции OR.

& Тест. 2.3.1. Укажите результат, выдаваемый программой 1). 1, 2) 2.

x=2: y=4: z=3

if x>y or y>z then print 1 else print 2

@ Контрольная задача. В устройстве ввода ЭВМ подготовлено четыре произвольных числа: A,B,C,D. ЭВМ должна ответить на вопрос: Правда ли что...? (вопрос берется из таблицы). Ответ ЭВМ должна вывести в виде текста: слова ”Правда” или ”Неправда”. Составить блок-схему, программы. Сделать проверку для произвольных аргументов.

Вопрос

Все числа положительны?

Ни одно из чисел не превышает число 90?

Каждое из первых двух чисел больше каждого из последних двух?

Первое число меньше остальных?

Эти числа расположены в возрастающей последовательности?

Эти числа расположены в убывающей последовательности?

Среди этих чисел есть равные?

Среди этих чисел нет равных?

Первое число не самое маленькое?

Все четыре числа равны между собой?

В простых примерах, рассмотренных выше, вообще говоря, не требо­валось привлечения ЭВМ и программирования. Все они достаточно быстро могли быть решены вручную или с помощью калькулятора. Сила ЭВМ заключается в возможности простыми средствами осуществлять многократное повторение заданных действий – циклов.

¶ИТЕРАЦИОННЫЕ ЦИКЛЫ. В случае, если количество циклов, необходимых для решения задачи, заранее неизвестно, такие циклы называются итерационными. Рассмотрим ряд примеров.

Задача 3. Пусть для некоторого множества чисел Х нужно вычислить и отпечатать функцию 2/Х. Ввод и вычисления следует прекратить после обнаружения первого Х, равного нулю (деление на ноль невозможно).

		Программа к задаче 3 3 INPUT x IF x=0 GOTO 9 y=2/x PRINT x y GO TO 3 9 END

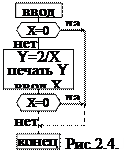Очевидна следующая блок-схема (рис. 2.4.1). Блоков ввода, вычисления, печати и анализа столько, сколько чисел в последовательности до первого нуля. Чисел может быть очень много и подобный подход, конечно, неприемлем, не говоря уже о том, что и количество их заранее неизвестно. Такие программы строятся по-иному. Обрабатывающая часть программы записывается только раз, но охватывается петлей возврата (рис. 2.4.2). Тогда одни и те же операторы будут выполняться многократно до тех пор, пока Х¹0.

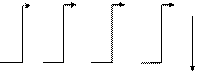
Задача 4. Пусть для аргумента Х, находящегося в диапазоне от 3 до 9, требуется вычислить и напечатать значение функции Y=(X–6)2, где Х изменяется с шагом 2 (рис. 2.4.3). Блок-схема алгоритма изображена на рис. 2.4.4.

Справа от текста программы сделаны выкладки по проверке решения. В каждой строке вручную вычисляется и указывается значение соответствующей переменной. Выкладки по проверке выполняются сверху-вниз, слева-направо по ходу исполнения программы. Стрелки показывают связи между циклами. Видим, что заданная последовательность изменения Х (3, 5, 7,...) наблюдается и последнее значение Y вычисляется для Х=9. При следующем приращении Х оно становится равным 11 и пятый цикл не выполняется, поскольку при Х>9 программа завершается.

Здесь следует отметить, что нет никакого технически простого способа предварительной проверки правильности написанных программ. Для этой цели программисту приходится вручную по тексту программы рассчитывать значения всех переменных и сличать их с желаемыми (известными из условия). Конечно, проверка выполняется не для всей задачи, а только для небольшого числа (например, трех) начальных циклов и при этом тщательно анализируется значение условия выхода из цикла (оператор IF).

Контрольная задача. Пусть дана функция Y=10–2X. ЭВМ должна вычислить и напечатать значения этой функции для последовательных значений Х: 0, 0.5, 1, 1.5, 2, 2.5,... и т.д. до тех пор, пока Y не станет отрицательным.

Программа	Проверка
к задаче 4	1 цикл	2 цикл	3 цикл	4 цикл
x=3 2 IF x>9 GOTO 4 y=(x–6)^2 ? x,y x=x+2 GOTO 2 4 END	x=3 x=3<9 y=9 3,9 x=3+2=5	5<9 y=1 5,1 x=7	7<9 y=1 7,1 x=9	9=9 y=9 9,9 x=11	11>9 конец

АРИФМЕТИЧЕСКИЕ ЦИКЛЫ. Если число повторений известно заранее – такие циклы называются арифметическими.

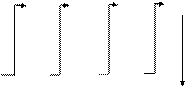
Задача 5. Пусть в условиях предыдущей задачи 4 не известно предельное значение аргумента, но зато задано количество точек аргумента – 4. Поскольку в данном случае не задано последнее значение Х, признак окончания циклов придется формировать самим. Для этого вводится переменная, которая фиксирует число уже выполненных циклов, т.е. счетчик циклов (назовем ее I). В исходном состоянии (рис. 2.4.5) берем его равным 1.

Программа	Проверка
к задаче 5	1 цикл	2 цикл	3 цикл	4 цикл
x=3: i=1 8 IF i>4 GOTO 2 y=(x–6)^2 ? x y x=x+2 i=i+1 GO TO 8 2 END	x=3, i=1 i=1<4 y=9 3, 9 x=5 i=2	2<4 y=1 5, 1 x=7	3<4 y=1 7, 1 x=9	4=4 y=9 9, 9 x=11	5>4 конец

После выполнения очередного цикла счетчик получает приращение, увеличиваясь на единицу (I=I+1). В начале каждого цикла в операторе IF делается проверка на достижение счетчиком последнего разрешенного значения (у нас 4). Если I<=4 программа продолжает вычисление функции, если нет (I>4) – счет прекращается. Ниже приведена программа и выкладки по ее проверке. Как видим, результат проверки совпал с результатом, полученным ранее. Исходное значение счетчика циклов и его приращения могут выглядеть по-разному. Главное, чтобы было выполнено заданное число циклов. В нашем примере был использован счетчик на возрастание I=1,2,3,... до N (N – число шагов). Можно начинать счетчик с нуля: I=0,1,2,... до N-1. Возможен счетчик на убывание: I=N–1,... 3,2,1 до 0 и т.д. Обычно, если нет оснований для другого, используется счетчик на возрастание с шагом единица от 1 до N.

ЗАДАЧИ НА НАКОПЛЕНИЕ. В практике очень распространены задачи на накопление, т.е. на нахождение сумм и произведений последовательности переменных. Такие задачи могут встречаться как в формулировке итерационных, так и арифметических циклов.

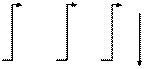
Задача 6. Пусть требуется найти сумму N произвольных чисел Х. Блок-схема алгоритма приведена на рис. 2.4.6, а программа ниже. Здесь сумма накапливается в переменной S с помощью оператора S=S+X. Начальное значение суммы берется равным нулю (S=0).

Программа	Проверка для N=3 X=2,4,3
к задаче 6	1 цикл	2 цикл	3 цикл
INPUT “N=”,n i=1: s=0 3 IF i>n GOTO 8 INPUT “X=”,x s=s+x i=i+1 GOTO 3 8 PRINT s	n=3 i=1, s=0 1<3 x=2 s=2 i=2	2<3	3=3	4>3 s=9

ЧИСЛОВЫЕ РЯДЫ. Типичной циклической задачей на накопление является вычисление числовых рядов.

Задача 7. Пусть требуется найти сумму S для N членов геометрической прогрессии вида

Дата добавления: 2014-12-27