Решение. 1. Сумма ежегодного платежа равна 100/5 = 20,0 млн

Решение

Решение

1. Сумма ежегодного платежа равна 100/5 = 20,0 млн. руб.

2. Определяем сумму процентных платежей для каждого года из пяти лет, млн. руб.:

1-го: 100 ∙ 0,06 = 6,0;

2-го: (100 – 6,0) ∙ 0,06 = 5,64;

3-го: (100 – (46,0 + 5,64)) ∙ 0,06 = 5,3;

4-го: (100 – (6,0 + 5,64 + 5,3)) ∙ 0,06 = 4,98;

5-го: (100 – (6,0 + 5,64 + 5,3 + 4,98)) ∙ 0,06 = 4,73.

3. Определяем сумму поручений (срочных уплат) по годам при условии погашения долга равными долями для каждого года, млн. руб.:

1-го: 20 + 6,0 = 26,0;

2-го: 20 + 5,64 = 25,64;

3-го: 20 + 5,3 = 25,3;

4-го: 20 + 4,98 = 24,98;

5-го: 20 + 4,73 = 24,73.

4. Находим средний срок погашения долга (аннуитет) по простым процентам:

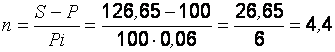года.

Пример 2.5. Как изменяется общая процентная ставка трех вариантов с разными соотношениями вкладов (0,6 и 0,4; 0,4 и 0,6; 0,5 и 0,5) при увеличении банковского процента по первому виду вкладов в 1,2 раза и уменьшении по второму в 0,8 раза.

Общая ставка равна, %:

1-й вариант:

1,2 ∙ 0,6 + 0,8 ∙ 0,4 = 1,04;

2-й вариант:

1,2 ∙ 0,4 + 0,8 ∙ 0,6 = 0,96;

3-й вариант:

1,2 ∙ 0,5 + 0,8 ∙ 0,5 = 1,0.

Пример 2.6. Имеется ряд прямых чисел: 1,01; 1,05; 1,1; 1,2; 1,25; 2,0. Каков будет ряд обратных чисел? Почему приращения прямых и обратных чисел различаются по величине? Каков закон асимметрии? Почему нельзя приращения умножать и делить друг на друга, складывать и вычитать?

Расчетные обратные числа:

1/0,01 = 0,9901: 1/1,05 = 0,9412;

1/1,1 = 0,9091: 1/1,2 = 0,833;

1/1,25 = 0,8;

1/2 = 0,5.

Различие приращений прямых и обратных чисел объясняется действием закона асимметрии, в основе которого лежат различия между расчетами сложных процентов «со ста» и «на сто».

С увеличением абсолютного значения 1 % прироста (например, вклада) разница между прямыми и обратными приращениями увеличивается. При минимальных значениях приращения эта разница ничтожна (при приросте 1 % она составляет 0,001 %). На этом основании обычно игнорируют различия между приращениями прямых и обратных чисел, что неверно, поскольку правило процентных исчислений строится для общего случая, который указывает на существование сколь угодно больших различий между ними.

Над приращениями прямых и обратных чисел нельзя производить обычные арифметические действия, поскольку они соответствуют различным точкам отчета и связаны между собой через произведение или частное от деления целых процентных чисел, по отношению к которым выступают частями.

Пример 2.7. Имеются следующие данные (табл. 2.2).

Таблица 2.2

Прирост трех различных показателей за два периода и увеличение,

исчисленное в двух вариантах, %

Номер показателя	Темп прироста	Вариант расчета увеличения прироста
1-й период	2-й период	1-й	2-й
			16 – 6 = 10 19 – 17 = 2 24 – 20 = 4	(1,16/1,06 – 1) – 100 = 9,4 (1,19/1,17 – 1) – 100 = 1,7 (1,24/1,2 – 1) – 100 = 3,3

Какой из представленных вариантов расчета увеличения прироста показателей является верным?

Дата добавления: 2014-12-27