Решение. Реализация товара В данного торгового дня на различных субрынках

Реализация товара В данного торгового дня на различных субрынках

Субрынок	Цена, руб./кг	Объем продаж	Выручка от реализации	На территориях, обслуживаемыхсубрынками, проживает
тыс. руб.	удельный вес, %	тыс. руб.	удельный вес, %	население, тыс. чел.	семей, тыс.
А
I II III		5,5 6,8 4,4	32,93 40,72 26,35	66,0 122,4 61,6	26,40 48,96 24,64	12,75 18,27 21,12	5,1 6,3 6,6
Итого	–	16,7		250,0		52,14	18,0

Вычислите среднюю цену на товар данного торгового дня при условии, что имеются сведения, указанные в графах табл. 2.10:

1) только гр. 1;

2) гр. 1 и 2;

3) гр. 1 и 3;

4) гр. 1 и 4;

5) гр. 1 и 5;

6) гр. 1 и 6;

7) гр. 1 и 7.

Сравните полученные результаты. Дайте оценку их точности. Объясните причины расхождения.

1.

2.

3.

4.

5.

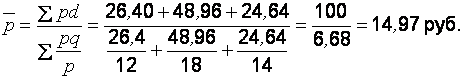
6.

7. ,

где – средняя цена; q – объем продаж; pq – выручка от реализации;
d – удельный вес объема продаж и выручки от реализации; S – численность населения; F – число семей.

Средние цены в п. 2, 3, 4, 5 решения совпали, поскольку являются наиболее точным уровнем средних цен на данный торговый день.
Остальные цены отличаются от цен, рассчитанных в п. 2, 3, 4 и 5, так как были рассчитаны без взвешивания (п.1) либо с использованием не прямых, а косвенных показателей в качестве весов.

2.4.3. Статистическое изучение динамики цен

В экономике применяются оптовые, розничные, закупочные, сметные и другие цены.

Одним из направлений анализа цен является изучение уровней цен в динамике. Для этого применяются индивидуальные и общие индексы цен Пааше и Ласпейреса и др. Индивидуальный индекс цен характеризует изменение цены на один товар (услугу).

Общие индексы цен дают обобщающую характеристику части или совокупности цен.

Индексы цен Пааше рассчитываются по формуле

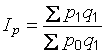. (2.7)

Индексы цен, рассчитанные по формуле Пааше, охватывают широкий круг товаров и услуг и используются при измерении динамики розничных цен, закупочных цен в сельском хозяйстве, сметных цен в строительстве, цен компонентов ВВП и др.

Индексы цен Ласпейреса рассчитываются по формуле

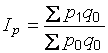(2.8)

и применяются при вычислении индексов потребительских цен. ИПЦ, рассчитанный по формуле Ласпейреса, показывает, как изменились бы потребительские расходы в текущем периоде по сравнению с базисным, если бы уровень и структура потребления остались без изменений.

Формулы индексов цен (2.7), (2.8) записаны в агрегатной форме.

Индексы цен Пааше и Ласпейреса могут быть рассчитаны по формулам средних из индивидуальных индексов.

Индекс цен Паше

– средняя гармоническая. (2.9)

Индекс цен Ласпейреса

– средняя арифметическая. (2.10)

Сводный индекс потребительских цен рассчитывается по формуле

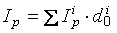, (2.11)

где – индексы потребительских цен по отдельным группам товаров и услуг; – доля каждой группы товаров в общем объеме потребительских расходов населения в базисном периоде.

Доля каждой группы товаров в общем объеме потребительских расходов

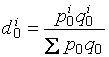. (3.12)

Если данные об указанных весах неизвестны, то в качестве весов могут использоваться другие показатели: численность населения или число домохозяйств, проживающих на данной территории, обслуживаемых определенным субрынком.

В статистике наряду с изучением уровня цен на отдельные товары возникает необходимость расчета динамики средних цен. Для характеристики динамики средних цен и факторов, влияющих на них, используется система индексов: индексы цен переменного состава, постоянного состава и структурных сдвигов.

Индекс цен переменного состава

, (2.13)

или

. (2.14)

Индекс цен постоянного состава

, (2.15)

или

. (2.16)

Индекс цен структурных сдвигов

, (2.17)

или

. (2.18)

Индексы взаимосвязаны между собой:

. (4.16)

Абсолютное изменение средней цены

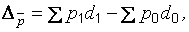
в том числе за счет изменения:

– цен

;

– структуры

;

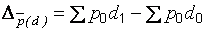– двух факторов

Для расчета индексов цен помимо традиционных используются и другие методы. Например, для однородных товаров и (услуг) могут быть вычислены простейшие агрегатные индексы (субиндексы) по различным методикам:

Дюто

; (2.20)

Карли

; (2.21)

по формуле средней геометрической

. (2.22)

Для разноименных товаров (услуг) помимо общеизвестных также вычисляются индексы по следующим методикам:

Эджворта – Маршалла

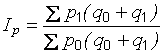; (2.23)

Фишера («идеальная» формула)

(2.24)

Пример 2.19. Имеются следующие данные (табл. 2.11).

Таблица 2.11

Дата добавления: 2014-12-27