Расчет сложных цепей с помощью уравнений Кирхгофа

Пример 1
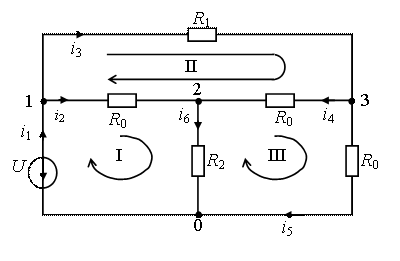
Далеко не во всех случаях цепь представляет собой совокупность лишь последовательно и параллельно соединенных ветвей. В качестве примера рассмотрим вариант расчета с помощью уравнений Кирхгофа электрической цепи (рисунок 10). Цепь содержит = 4 узлов и 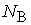= 6 ветвей, включая источники напряжения.

R ₁

R ₀

R ₀

R ₀

R ₂

U

i ₁

i ₂

i ₃

i ₄

i ₆

i ₅

III

I

II

Рис.10.
Для определения всех токов и напряжений в схеме достаточно найти значения токов во всех ветвях цепи. Зная ток, проходящий через любую из ветвей цепи, можно найти как напряжение этой ветви, так и напряжение между любой парой узлов цепи.
Если мы зададимся произвольно положительными направлениями токов в ветвях цепи и пронумеруем произвольно эти токи, то по первому закону Кирхгофа можно составить 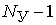уравнений относительно токов в ветвях цепи.
По второму закону Кирхгофа будет 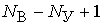линейно-независимых уравнений для напряжений 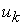ветвей схемы.
Совокупность из 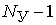уравнений по первому закону Кирхгофа, и 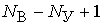уравнений, составленных по второму закону Кирхгофа, образует систему 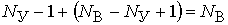линейно – независимых уравнений. Эта система будет неоднородной системой уравнений, так как ее свободными членами являются заданные напряжения источников.

Подобная система уравнений имеет единственное решение, позволяющее найти токи в ветвях цепи, а по ним и значения напряжений между любой парой узлов цепи.
Для примера составим систему уравнений по первому закону Кирхгофа (рисунок 10).
Число уравнений: .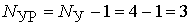
Узел 1: ,
узел 2: ,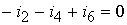
узел 3: .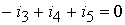
В тоже время по второму закону Кирхгофа для контуров I, II, III можно составить систему из 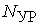уравнений.
.
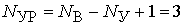Контур I: ,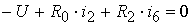
контур II: ,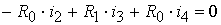
контур III: .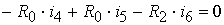
Таким образом, решая систему из 6 уравнений с шестью неизвестными токами, например по методу Крамера, определим неизвестные. Если в цепи будет источник тока, то в системе уравнений неизвестным будет напряжение на зажимах этого источника, а ток через источник будет равен току задающего источника. Общее число неизвестных сохранится прежним.

Дата добавления: 2015-04-24