Закон исключенного третьего

Онтологическим аналогом этого закона является то, что в предмете указанный признак присутствует или его нет, поэтому и в мышлении мы отражаем это обстоятельство в виде закона исключенного третьего.

В книге “Метафизика” Аристотель сформулировал закон ис­ключенного третьего так: “Равным образом не может быть ни­чего промежуточного между двумя членами противоречия, а относительно чего-то одного необходимо что бы то ни было одно либо утверждать, либо отрицать”1.

В двузначной традиционной логике закон исключенного треть­его формулируется так: ”Из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано”. Проти­воречащими (контрадикторными) называются такие два суж­дения, в одном из которых что-либо утверждается о предмете, а в другом то же самое об этом же предмете отрицается, поэто­му они не могут быть оба одновременно истинными и оба лож­ными; одно из них истинно, а другое обязательно ложно. Такие суждения называются отрицающими друг друга. Если одно из противоречащих суждений обозначить переменной а, то другое следует обозначить a. Так, из двух суждений: “Джеймс Фенимор Купер является автором серии романов о Кожаном Чулке, сдававшихся на протяжении почти 20 лет” и “Джеймс Фенимор Купер не является автором серии романов о Кожаном Чулке, создававшихся на протяжении почти 20 лет” первое истинно, второе ложно, и третьего - промежуточного - суждения не может быть.

Отрицающими являются следующие пары суждений:

1) “Это S есть Р” и “Это S не есть Р” (единичные суждения).

2) “Все S есть Р” и “Некоторые S не есть Р” (суждения А и О).

3) “Ни одно S не есть Р” и “Некоторые S есть Р” (суждения Е и І).

В отношении противоречащих (контрадикторных) суждений (А и О, Е и I) действует как закон исключенного третьего, так и закон непротиворечия - в этом одно из сходств данных законов.

Различие в областях определения (т. е. применения) этих зако­нов в том, что по отношению противных (контрарных) суждений А и Е (например: “Все грибы - съедобны” и “Ни один гриб не является съедобным”), которые оба не могут быть истинными, но оба могут быть ложными, распространяется действие лишь закона непротиворечия и не распространяется действие закона исключенного третьего. Итак, сфера действия содержательно­го закона непротиворечия шире (это контрарные и контрадик­торные суждения), чем сфера действия содержательного зако­на исключенного третьего (лишь контрадикторные, т. е. суждения типа а и не-а). Действительно, истинно одно из двух суждений:

“Все дома в данной деревне электрифицированы” или “Некото­рые дома в данной деревне не являются электрифицированными” и третьего не дано.

Закон исключенного третьего и в содержательном, и в форма­лизованном виде охватывает один и тот же круг суждений -противоречащие, т. е. отрицающие друг друга.

Содержательные аристотелевские законы непротиворечия и исключенного третьего невыводимы один из другого, так как области определения суждений, для которых они применимы, различные.

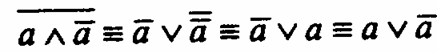
В силу того, что в формализованных законах непротиворечия и исключенного третьего, т. е. в формулах и а v a, области определения пропозициональных переменных (т. е. переменных, обозначающих суждение и его отрицание: а и a) оказываются одними и теми же (берутся лишь противоречащие суждения), то на основании закона де Моргана, т. е. формулы в = v , за­кона снятия двойного отрицания, т. е. a s а и закона коммута­тивности дизъюнкции, т. е. формулы (а v b) = (b v а), в двузнач­ной классической логике, путем элементарных эквивалентных преобразований из закона непротиворечия можно вывести закон исключенного третьего (и наоборот):

В мышлении закон исключенного третьего предполагает чет­кий выбор одной из двух взаимоисключающих альтернатив. Для корректного ведения дискуссии выполнение этого требования обязательно.

Дата добавления: 2015-04-24