Экзаменационный билет № 4. Основной постулат химической кинетики

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 3

Основной постулат химической кинетики

1867 г. Гульдберг, Вааге – закон действующих масс:

скорость элементарной реакции пропорциональна произведению концентраций реагирующих веществ в степенях их стехиометрических коэффициентов

aA + bB → сС + dD

V=k[A]^a[B]^b

1. Понятие о дисперсных системах. Дисперсная фаза, дисперсионная среда. Классификации и примеры дисперсных систем.

2. Защитные покрытия металлов от коррозии. Анодные и катодные покрытия.

Ответ:

Дисперсными называют такие системы, в которых одно или несколько веществ в виде мелких частиц распределены в другом веществе.

При этом распределяемое вещество принято называть дисперсной фазой, а вещество, в котором происходит распределение, - дисперсной средой.

Дисперсные системы	Размеры частиц дисперсной системы	Устойчивость и гомогенность системы
Грубодисперсные (суспензии, взвеси)	10-3…10-5 см (10…0,1 мкм)	Неустойчивы, гетерогенны
Тонкодисперсные (коллоидные растворы)	10-5…10-7 см (0,1…0,001 мкм)	Довольно устойчивы, микрогетерогенны
Молекулярно-дисперсные (истинные растворы)	~10-8 см (размер молекул и ионов)	Весьма устойчивы, гомогенны

Дисперсная среда	Дисперсная фаза	Примеры
Газ	газ жидкость твердое тело	газовые смеси (воздух) туманы, облака пыль, дым
Жидкость	газ жидкость твердое тело	пена эмульсии (молоко, кремы, мази), суспензии, взвеси (глина в воде)
Твердое тело	газ   жидкость   твердое тело	твердые пены(пенопласты, пемза, пеностекло) твердые эмульсии (вода в парафине, жемчуг) сплавы, твердые растворы

Защитные покрытия:

Металлические

Химические

Неметаллические

- Неорганические (эмали)

- Органические (лаки, краски, пластмассы, смолы, битум, асфальт)

Анодное покрытие – покрытие металлом, с более отрицательным потенциалом

Оцинкованное железо

А(–) Zn – 2e^– → Zn²⁺

K(+) (Fe) 2H⁺ + 2e^– → H₂

Катодное покрытие – покрытие металлом, с более положительным потенциалом

Луженое железо

А(–) Fe – 2e^– → Fe²⁺

K(+) (Sn) 2H⁺ + 2e^– → H₂

1. Основные положения квантовой механики: уравнение де Бройля, принцип неопределен­ности Гейзенберга, уравнение Шредингера.

2. Свойства разбавленных растворов неэлектролитов (законы Рауля).

Ответ:

В 20-х годах XX столетия было установлено, что любая частица имеет корпускулярно-волновую природу. Согласно теории Л. де Бройля (1924 г.), каждой частице с импульсом соответствует волновой процесс с длиной волны λ, т.е. λ = h / p. Чем меньше масса частицы, тем больше длина волны. Для элементарных частиц В. Гейзенберг сформулировал принцип неопределенности, согласно которому невозможно одновременно определить положение частицы в пространстве и ее импульс. Следовательно, нельзя рассчитать траекторию движения электрона в поле ядра, можно лишь оценить вероятность его нахождения в атоме с помощью волновой функции ψ, которая заменяет классическое понятие траектории. Волновая функция ψ характеризует амплитуду волны в зависимости от координат электрона, а ее квадрат ψ² определяет пространственное распределение электрона в атоме. В наиболее простом варианте волновая функция зависит от трех пространственных координат и дает возможность определить вероятность нахождения электрона в атомном пространстве или его орбиталь. Таким образом, атомная орбиталь (АО) – область атомного пространства, в котором вероятность нахождения электрона наибольшая. Волновые функции получаются при решении основополагающего соотношения волновой механики – уравнения Шредингера. Пусть волновая функция задана в N-мерном пространстве, тогда в каждой точке с координатами 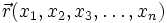, в определенный момент времени t она будет иметь вид 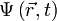. В таком случае уравнение Шрёдингера запишется в виде:

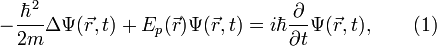
где 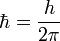, 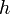— постоянная Планка; 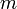— масса частицы, 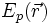— внешняя по отношению к частице потенциальная энергия в точке 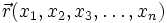, 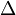— оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла.

(Точное решение получается для атома водорода или водородоподобных ионов, для многоэлектронных систем используются различные приближения). Поверхность, ограничивающая 90–95 % вероятности нахождения электрона или электронной плотности, называют граничной. Атомная орбиталь и плотность электронного облака имеют одинаковую граничную поверхность (форму) и одинаковую пространственную ориентацию. Атомные орбитали электрона, их энергия и направление в пространстве зависят от четырех параметров – квантовых чисел.

Дата добавления: 2015-04-24