Экзаминационые ответы по алгебре и геометрий

1). Комплексные числа: определения, геометрическая интерпретация, действия в алгебраической, тригонометрической и показательной формах

Определение комплексного числа (Сформулируйте определение комплексного числа)

Комплексным числом z называется выражение следующего вида:

Комплексное число в алгебраической форме,(1)

Где x, y ;

i — это мнимая единица, определяемая равенством i2 = –1.

Основные термины:

x = Re z — действительная часть комплексного числа z;

y = Im z — мнимая часть комплексного числа z;

— комплексно сопряженное число числу z;

— противоположное число числу z;

— комплексный ноль;

– так обозначается множество комплексных чисел.

Примеры

1)z = 1 + i  Re z = 1, Im z = 1, = 1 – i, = –1 – i;

2)z = –1 + i  Re z = –1, Im z =, = –1 – i, = –1 – i;

3)z = 5 + 0i = 5  Re z = 5, Im z = 0, = 5 – 0i = 5, = –5 – 0i = –5

 если Im z = 0, то z = x — действительное число;

4)z = 0 + 3i = 3i  Re z = 0, Im z = 3, = 0 – 3i = –3i, = –0 – 3i = – 3i

 если Re z = 0, то z = iy — чисто мнимое число.

Комплексные равенства (Сформулируйте смысл комплексного равенства) Комплексные числа: определения, геометрическая интерпретация, действия в алгебраической, тригонометрической и показательной формах

Определение комплексного числа (Сформулируйте определение комплексного числа)

Комплексным числом z называется выражение следующего вида:

Комплексные числа: определения, геометрическая интерпретация, действия в алгебраической, тригонометрической и показательной формах.

Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть и φ = arg z. Тогда по определению аргумента имеем:

тригонометрическую формы числа z = z1 + z2. Изобразить числа z1, z2 и z на комплексной плоскости. Вычислить z12 по формуле Муавра.

корни с тепени:

1). 1.Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей с тем же показателем:

(abc...)n=anbncn...

Практически более важно обратное преобразование:

anbncn...=(abc...)n,

т.е. произведение одинаковых степеней нескольких величин равно той же степени произведения этих величин.

2.Степень частного (дроби) равна частному от деления той же степени делимого на ту же степень делителя:

3.При умножении степеней с одинаковыми основаниями показатели степеней складываются:

aman=am+n

4.При делении степеней с одинаковыми основаниями показатель степени делителя вычитается из показателя степени делимого:

am/an=am-n

5.При возведении степени в степень показатели степеней перемножаются:

(am)n=amn.

2). Корень -й степени из числа — это число, -я степень которого равна.

Если — чётно.

Тогда, если a < 0 корень n-ой степени из a не определен.

Или если a ≥ 0, то неотрицательный корень уравнения называется арифметическим корнем n-ой степени из a и обозначается

Если — нечётно.

3). Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй.

(a+b)2=a2+2ab+b2

Квадрат разности двух величин равен квадрату первой минус удвоенное произведение первой на вторую плюс квадрат второй.

(a-b)2=a2-2ab+b2

Произведение суммы двух величин на их разность равно разности их квадратов.

(a+b)(a-b)=a2-b2

Куб суммы двух величин равен кубу первой плюс утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй плюс куб второй.

(a+b)3=a3+3a2b+3ab2+b3

Куб разности двух величин равен кубу первой минус утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй минус куб второй.

(a-b)3=a3-3a2b+3ab2-b3

Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов.

(a+b)(a2-ab+b2)=a3+b3

Произведение разности двух величин на неполный квадрат суммы равно разности их кубов.

(a-b)(a2+ab+b2)=a3-b3

Функция, и их свойства и графики:

1) Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной x однозначно определяет значение выражения x2, а значение месяца однозначно определяет значение следующего за ним месяца, также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.

Часто под термином «функция» понимается числовая функция; то есть функция которая ставит одни числа в соответствие другим. Отчетливое выявление основных свойств, позволяющих достаточно наглядно судить о ее поведении, называют исследованием функции.

В стандартную схему исследования функции обычно включают следующие пункты.

1. Область определения функции.

2. Нули (корни) функции.

3. Промежутки знакопостоянства.

4. Точки экстремума функции.

5. Промежутки возрастания и убывания (монотонность) функции.

6. Наибольшее и наименьшее значения функции.

7. Множество значений функции.

2) Функция, заданная формулой y = ax2 + bx + c, где x и y - переменные, а a, b, c - заданные числа, причем a=0, называется

квадратичной функцией.

График квадратичной функции - парабола. Если a > 0, то ветви параболы направлены вверх. Если a < 0, то ветви параболы направлены вниз.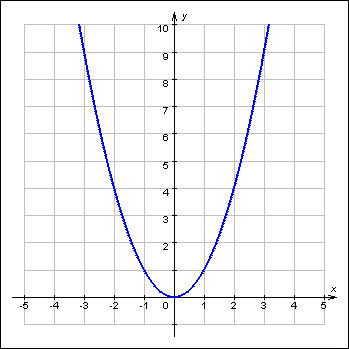

Уравнение и неравенство,

1) Линейным уравнением с одной переменной x называется уравнение вида ax+b=0, где a и b – некоторые числа.

Решить уравнение – значит найти все его корни или доказать, что корней нет. Линейным уравнением называется уравнение вида

ax + b = 0 и любое другое уравнение приводимое к такому виду (например, ax + b = cx + d).

Здесь буквой x(икс) обозначена неизвестная переменная, а буквами a,b - числа. Их называют коэффициентами линейного уравнения:

a - коэффициент при неизвестной,

b - свободный член.

Решить уравнение значит найти такое число(корень уравнения), что при подстановке его вместо переменной x, получается верное равенство.

Примеры линейных уравнений:

2x + 1 = 0. Корень(решение) этого уравнения

− 3x + 1 = x − 7. Корень этого уравнения x = 2

2) Определение.

Квадратным уравнением называют уравнение вида ах+вх+с=0, где х - неизвестное, а, в, с - действительные числа, где: а0.

Родовое понятие - уравнение.

Видовые отличия:

1) имеет вид ах+вх+с=0

(х - неизвестное; а, в, с - действительные числа);

2) а0. Дискриминант

Определение

Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D < 0, корней нет;

Если D = 0, есть ровно один корень;

Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают.

3) Основным методом решения неравенств вида (1) является метод интервалов. Начнём рассматривать его, прежде всего, для многочленов. Этот метод основан на том, что двучлен (x – a) положителен при x > a и отрицателен при x < a, то есть при переходе через точку x = a этот двучлен меняет знак.

Отсюда следуют полезные замечания. Если на интервале (a; b) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак.

Пусть функция f непрерывна на интервале I и обращается в нуль в конечном числе точек этого интервала. По сформулированному выше свойству непрерывных функций этими точками I разбивается на интервалы, в каждом из которых непрерывная функция F сохраняет постоянный знак.

Чтобы определить этот знак, достаточно вычислить значение функции f в какой-либо одной точке из каждого такого интервала.

Дата добавления: 2015-04-24