Геометрия

1) Взаимное расположение двух прямых в пространстве

Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями.

Прямые лежат в одной плоскости и не имеют общих точек — параллельные прямые.

Прямые лежат и одной плоскости и имеют одну общую точку — прямые пересекаются.

В пространстве две прямые могут быть расположены еще так, что не лежат ни в одной плоскости. Такие прямые называются скрещивающимися (не пересекаются и не параллельны).

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость и точке, которая не лежит на первой прямой, то эти прямые скрещиваются.

прямая a лежит в плоскости, а прямая с пересекает в точке N. Прямые a и с — скрещивающиеся.

Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой.

прямые a и b скрещиваются. Черен прямую а проведена плоскость || b (в плоскости указана прямая a1 || b).

Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты.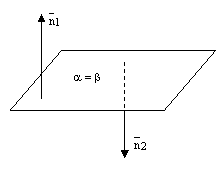

2)

Прямая может принадлежать и не принадлежать плоскости. Она принадлежит плоскости, если хотя бы две точки ее лежат на плоскости. На рис. 93 показана плоскость Sum (axb). Прямая l принадлежит плоскости Sum, так как ее точки 1 и 2 принадлежат этой плоскости.

Если прямая не принадлежит плоскости, она может быть параллельной ей или пересекать ее.

Прямая параллельна плоскости, если она параллельна другой пря-

мой, лежащей в этой плоскости. На рис. 93 прямая т || Sum, так как она параллельна прямой l, принадлежащей этой плоскости.

Прямая может пересекать плоскость под различными углами и, в частности, быть перпендикулярной ей. Построение линий пересечения прямой с плоскостью приведено в

Точка по отношению к плоскости может быть расположена следующим образом: принадлежать или не принадлежать ей. Точка принадлежит плоскости, если она расположена на прямой, расположенной в этой плоскости. На рис. 94 показан комплексный чертеж плоскости Sum, заданной двумя параллельными прямыми l и п. В плоскости расположена линия т. Точка A лежит в плоскости Sum, так как она лежит на прямой т. Точка В не принадлежит плоскости, так как ее вторая проекция не лежит на соответствующих проекциях прямой. 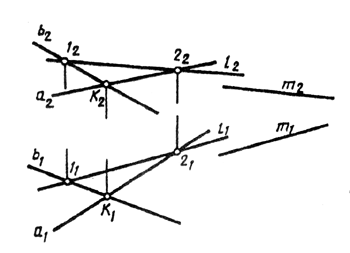К понятию о параллельных прямых следует подвести учащихся следующим образом. Учащимся предлагается провести произвольную прямую АВ, отметить на ней две близлежащие точки М и N и провести через эти точки к прямой АВ перпендикуляры ММ1 и NN1. Ставится вопрос, пересекутся ли эти перпендикуляры, если их продолжить в ту или другую сторону от прямой АВ.

Если на заданный вопрос последует ответ, что прямые не пересекутся, а это учащиеся чувствуют интуитивно, или, наоборот, будет дан ответ, что прямые пересекутся, необходимо указать учащимся, что каждое из сделанных ими утверждений должно быть доказано, т.е. обосновано ссылкой на известные им аксиомы и теоремы.

Доказательство: имеем ММ1 перпендикулярно АВ, NN1 перпендикулярно АВ. Докажем, что перпендикуляры ММ1 и NN1, проведенные к одной и той же прямой АВ, не могут пересечься. Предположим противное, а именно – что перпендикуляры ММ1 и NN1 пересекутся в некоторой точке О, тогда получается треугольник МОN, в котором сумма двух внутренних углов, Ð1 и Ð2, равна двум прямым: Ð1+Ð2=180, что невозможно, так как согласно сумма двух углов треугольника всегда меньше 180 градусов. Отсюда следует, что принятое допущение, что перпендикуляры ММ1 и NN1 при своем продолжении пересекутся в некоторой точке О, неверно. Итак, два перпендикуляра к одной и той же прямой не пересекаются, сколько бы их ни продолжать.

После такого разбора учащимся указывается, что на плоскости можно расположить две прямые так, что они никогда не пересекутся, и дается определение: прямые, которые расположены в одной плоскости и не пересекаются, называются параллельными.

Возвращаясь затем у полученному выше выводу о взаимном положении двух перпендикуляров к одной и той же прямой, преподаватель отмечает, что этот вывод можно формулировать в виде теоремы: две прямые, перпендикулярные к третьей, параллельны.

Вводится знак для обозначения параллельности двух прямых: АВ ççCD.

Преподаватель должен подчеркнуть, что необходимым условием для параллельности двух прямых является то, что прямые должны лежать в одной плоскости. Это указание должно быть выявлено в определении, а потому определение параллельных прямых без слов «которые расположены в одной плоскости» является неполным.

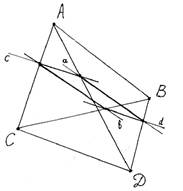
Следует использовать модель куба для показа параллельных и непараллельных прямых. Так, ребра куба АВ и А1D1 не пересекаются: они лежат в разных плоскостях; поясняется, что такие прямые, в отличие от прямых параллельных, называются скрещивающимися. ребра же куба АВ и А1В1, АА1 и ВВ1, ВВ1 и СС1 также не пересекаются; однако они попарно расположены на одной плоскости, они параллельны.

Теорема о двух перпендикулярах на плоскости к одной и той же прямой является одним из признаков параллельности прямых. Необходимо показать учащимся ее практическое приложение, для чего следует решить задачу:

На плоскости даны две точки А и В. Провести через эти точки две параллельные прямые.

Построение. Через точки А и В проводится прямая MN, и в этих же точках строятся к прямой MN перпендикуляры АС и BD (АС ççBD). Продолжая оба перпендикуляра по другую сторону от прямой MN имеем: СС1 çç DD1. Это одно из многочисленных решений; через точки А и В можно провести бесчисленное множество пар параллельных прямых.

Действительно, проводим на плоскости ряд произвольных прямых и к ним через точки А и В перпендикуляры. Получаем, что в каждой из точек А и В пучок прямых. При этом каждой прямой пучка с центром в точке А соответствует определенная прямая, ей параллельная, принадлежащая пучку с центром в точке В.

После этого следует решить задачу на построение. Через точку А вне данной прямой провести прямую, параллельную данной.

Запись задачи на доске: Дана прямая MN и вне ее точка А. Провести через точку А прямую, параллельную данной.

Решение. Из данной точки А проводят к прямой MN при помощи линейки и чертежного треугольника перпендикуляр АР. Затем проводят через точку А к прямой АР перпендикуляр АК также при помощи линейки и чертежного треугольника. Прямая АК параллельна MN на основании теоремы: две прямые, перпендикулярные к третьей, параллельны.

Необходимо предложить учащимся сделать несколько построений, различно расположив прямую MN относительно края доски или листа бумаги.

Когда построение выполнено, преподаватель должен указать, что необходимо еще исследовать, нет ли помимо построенной прямой еще другой прямой, которая также проходит через точку А и параллельна данной прямой MN, и что если таковой нет, то проведенная прямая является единственной прямой, проходящей через точку А параллельно прямой MN.

Учащимся разъясняется, что доказать это положение нельзя при помощи известных нам аксиом и теорем и что вековой опыт человечества, приобретенный решением практических задач, привел еще древних геометров к заключению, что через данную точку вне прямой на плоскости можно провести только одну прямую, параллельную данной прямой.

Последнее суждение есть аксиома о параллельных.

Не лишнее указать учащимся, что, начиная с древнейших времен, лучшими математиками все же делались попытки доказать аксиому о параллельных, т.е. рассматривать ее как теорему, которая, как они предполагали, может быть доказана при помощи уже принятых аксиом. Однако их попытки были и остались безуспешными. В настоящее время рассуждениями, выходящими за пределы элементарного курса геометрии, установлено, что аксиому о параллельных нельзя доказать без внесения дополнительных аксиом к числу тех, которые установлены Евклидом.

На аксиоме о параллельных и следствиях из нее следует заострить внимание учащихся.

Учащиеся должны уметь формулировать словами запись: на плоскости АВ çç CD и CDççMN, уметь сделать к ней нужный чертеж и после соответствующего доказательства записать вывод, вытекающий из взаимного расположения прямых АВ, CD и MN. А именно, что АВççMN. К чтению такого рода записей и учению по записи сделать соответствующий вывод следует приучать учащихся.

Большинство учебников обычно приводит аксиому о параллельных непосредственно перед рассмотрением обратной теоремы о параллельных, т.е. теоремы: две параллельные прямые, пересеченные третьей, образуют равные внутренние накрест лежащие углы, так как доказательство этой теоремы основано на аксиоме о параллельных. Для прямой теоремы: две прямые, пересеченные третьей, параллельны, если внутренние накрест лежащие углы равны – нет необходимости в применении аксиомы о параллельных. Для доказательства прямой теоремы достаточно предшествующих аксиом.

Приводя все же аксиому о параллельных ранее, а именно – в связи с анализом решения задачи о проведении прямой, параллельной данной прямой, полагаем, что при таком расположении материала учащимся более доступно понимание необходимости аксиомы о параллельных.

3) О ТРЕХ ПЕРПЕНДИКУЛЯРАХ.

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной.

И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Доказательство: Пусть АВ - перпендикуляр плоскости, АС - наклонная и с - прямая в плоскости, проходящая через основание С.

Проведем прямую СA1, параллельную прямой АВ. Она перпендикулярна плоскости. Проведем через прямые АВ и СA1 плоскость. Прямая с перпендикулярна прямой СA1. Если она перпендикулярна прямой СВ, то она перпендикулярна плоскости, а значит, и прямой АС.

АНАЛОГИЧНО. Если прямая с перпендикулярна наклонной АС то она, будучи перпендикулярна и прямой СA1 перпендикулярна плоскости, а значит, и проекции наклонной СВ. Теорема доказана.

4)

перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения.

ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ.

Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.

Доказательство.

5) Возможны два случая взаимного расположения двух плоскостей в пространстве:

Параллельны

Пересекаться

Опр. Две плоскости в пространстве называются параллельными, если они не пересекаются, в противном случаи они пересекаются.

Теорема1: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство:

Пусть и - данные плоскости, а1 и а2 - прямые в плоскости, пересекающиеся в точке А, в1 и в2 - соответственно параллельные им прямые в

плоскости. Допустим, что плоскости и не параллельны, т.е. пересекаются по некоторой прямой с. По теореме прямые а1 и а2, как параллельные прямым в1и в2, параллельны плоскости, и поэтому они не

пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости через точку А проходят две прямые (а1 и а2), параллельные прямой с. Но это невозможно по аксиоме параллельных. Мы пришли к противоречию ЧТД. Параллельность прямой и плоскости

Плоскость α и прямая a, не принадлежащая плоскости α, называются параллельными, если они не имеют ни одной общей точки. Любая прямая a, принадлежащая плоскости α, считается параллельной плоскости α. Если плоскость α и прямая a параллельны, то пишут α∣∣a или

a∣∣α.

Признак параллельности прямой и плоскости:

Если прямая параллельна какой-либо прямой, лежащей в плоскости, то данные прямая и плоскость параллельны.

Теоремы о плоскости и прямой, параллельной плоскости:

Если плоскость проведена через прямую, параллельную другой плоскости, и пересекает эту плоскость, то лилия пересечения плоскостей параллельна данной прямой.

Если через каждую из двух параллельных прямых проведена Произвольная плоскость и эти плоскости пересекаются, то линия их пересечения параллельна каждой из данных прямых.

Параллельность плоскостей. Две плоскости α и β называются параллельными, если они не имеют общей точки и не совпадают. Если плоскости α и β параллельны, то пишут ее α∣∣β.

Свойства параллельных плоскостей:

Любая плоскость считается параллельной самой себе (рефлексивность).

Если плоскость α параллельна плоскости β, то и плоскость β параллельна плоскости α (симметричность).

Если плоскость α параллельна плоскости β, а плоскость β параллельна плоскости γ то плоскость α параллельна плоскости γ (транзитивность).

6) Пусть прямая a является линией пересечения плоскостей α и β (чертеж 3.3.1). Пусть плоскость γ, перпендикулярная прямой a, пересекает плоскости α и β по прямым m и n, которые взаимно перпендикулярны, то есть γ α = m, γ β = n и m n. Такие плоскости α и β называются взаимно перпендикулярными.

Это определение не зависит от плоскости Действительно, если провести другую плоскость перпендикулярную прямой

По теореме о следах. Угол, образованный прямыми и угол, образованный прямыми и равны как углы с соответственно параллельными и одинаково направленными сторонами.

Пусть a α, a β, тогда β α. То есть, если плоскость β содержит прямую a, перпендикулярную плоскости α, то плоскости α и β перпендикулярны. Перпендикулярность прямых - Перпендикулярность плоскостей. Перпендикулярность прямых и плоскостей. c. Перпендикулярные прямые в пространстве. Перпендикулярность прямой и плоскости Перпендикуляр и наклонные Двугранный угол. m. k. Пересекающиеся. Скрещивающиеся. Перпендикулярность прямой и плоскости.

7) 2.Аксиомы стереометрии.

1.Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

2.Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости (прямая лежит в этой плоскости).

Из аксиомы следует, что если прямая имеет не более одной общей точки с плоскостью, то она не принадлежит этой плоскости. Если прямая и плоскость имеют только одну общую точку, то они пересекаются.

3.Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

В этом случае говорят, что плоскости пересекаются по прямой.

На рис. 1 плоскости α и β пересекаются по прямой a.

Записывают это обычно так: α∩β=a.

8) Существуют три случая взаимного расположения двух прямых в пространстве:

прямые лежат в одной плоскости и параллельны;

прямые лежат в одной плоскости и пересекаются;

прямые скрещиваются.

Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Теорема (признак скрещивающихся прямых):

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.

Доказательство:

Пусть,. Докажем, что и не лежат в одной плоскости. Предположим противное: через прямые a и b проходит некоторая плоскость в. Тогда в проходит через прямую а и точку, не принадлежащую этой прямой, а, значит, совпадает с плоскостью Y. Получили противоречие с условием (прямая). Значит предположение неверно и прямые a и b скрещивающиеся.

Теорема (о скрещивающихся прямых): через каждую из скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

9) Если две прямые пересекаются или параллельны, то они лежат в одной плоскости. Однако в пространстве две прямые могут быть расположены так, что они не лежат в одной плоскости, т. е. не существует такой плоскости, которая проходит через обе эти прямые. Ясно, что такие прямые не пересекаются и не параллельны.

Определение

Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а другая — под эстакадой (рис. 19).

Докажем теорему, которая выражает признак скрещивающихся прямых.

Теорема

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Дата добавления: 2015-04-24