Решение. В данной модели система ограничений состоит из одного линейного уравнения и нелинейной целевой функции

В данной модели система ограничений состоит из одного линейного уравнения и нелинейной целевой функции.

1. Заполняем ячейки на рабочем листе необходимыми переменными, целевой функцией и ограничениями:

2. В окне "Параметры поиска решения" сбрасываем флаги "Линейная модель" (так как решаемая задача есть задача нелинейного программирования)" и "Неотрицательные значения" (в условии задачи нет ограничений на знаки переменных).

3. После нажатия кнопки "Выполнить" получаем ответ:

из которого следует, что минимальное значение целевой функции равно 17278 и достигается при x₁ = 91 и x₂ = 89.

ЗАДАНИЕ 3

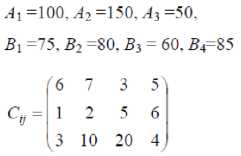Решить задачу транспортную задачу. Обозначения: Aj - запасы груза в i-м пункте отправления; Bj - потребности в грузе в j-м пункте назначения; C_ij - тарифы перевозок единицы груза из i-го пункта отправления в j-м пункт назначения.

Решение:

Математическая модель транспортной задачи:

F = ∑∑c_ijx_ij, (1)

при условиях:

∑x_ij = a_i, i = 1,2,…, m, (2)

∑x_ij = b_j, j = 1,2,…, n, (3)

С целью составления двойственной задачи переменные x_ij в условии (2) заменим на u₁, u₂, u_i,.., u_m, а переменные x_ij в условия (3) на v₁, v₂, v_j,.., v_n.

Поскольку каждая переменная x_ij входит в условия (2,3) и целевую функцию (1) по одному разу, то двойственную задачу по отношению к прямой транспортной задаче можно сформулировать следующим образом.

Требуется найти не отрицательные числа u_i (при i = 1,2,…,m) и v_j (при j = 1,2,..,n), обращающие в максимум целевую функцию

G = ∑a_iu_i + ∑b_jv_j

при условии

u_i + v_j ≤ c_ij, i = 1,2,..,m; j = 1,2,..,n (4)

В систему условий (4) будет mxn неравенств. По теории двойственности для оптимальных планов прямой и двойственной задачи для всех i,j должно быть:

u_i + v_j ≤ c_ij, если x_ij = 0,

u_i + v_j = c_ij, если x_ij ≥ 0,

Эти условия являются необходимыми и достаточными признаками оптимальности плана транспортной задачи.

Числа u_i, v_j называются потенциалами. Причем число u_i называется потенциалом поставщика, а число v_j – потенциалом потребителя.

По первой теореме двойственности в оптимальном решении значения целевых функций прямой и двойственных задач совпадают: F = G.

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов

					Запасы
Потребности

Проверим необходимое и достаточное условие разрешимости задачи.

∑a = 100 + 150 + 50 = 300

∑b = 75 + 80 + 60 + 85 = 300

Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.

Занесем исходные данные в распределительную таблицу.

					Запасы
Потребности

Поиск первого опорного плана.

1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел a_i, или b_j.

Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.

Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

Искомый элемент равен 1

Для этого элемента запасы равны 150, потребности 75. Поскольку минимальным является 75, то вычитаем его.

x₂₁ = min(150,75) = 75.

x
				150 - 75 = 75
x
75 - 75 = 0

Искомый элемент равен 2

Для этого элемента запасы равны 75, потребности 80. Поскольку минимальным является 75, то вычитаем его.

x₂₂ = min(75,80) = 75.

x
		x	x	75 - 75 = 0
x
	80 - 75 = 5

Искомый элемент равен 3

Для этого элемента запасы равны 100, потребности 60. Поскольку минимальным является 60, то вычитаем его.

x₁₃ = min(100,60) = 60.

x				100 - 60 = 40
		x	x
x		x
		60 - 60 = 0

Искомый элемент равен 4

Для этого элемента запасы равны 50, потребности 85. Поскольку минимальным является 50, то вычитаем его.

x₃₄ = min(50,85) = 50.

x
		x	x
x	x	x		50 - 50 = 0
			85 - 50 = 35

Искомый элемент равен 5

Для этого элемента запасы равны 40, потребности 35. Поскольку минимальным является 35, то вычитаем его.

x₁₄ = min(40,35) = 35.

x				40 - 35 = 5
		x	x
x	x	x
			35 - 35 = 0

Искомый элемент равен 7

Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.

x₁₂ = min(5,5) = 5.

x				5 - 5 = 0
		x	x
x	x	x
	5 - 5 = 0

					Запасы
		7[5]	3[60]	5[35]
	1[75]	2[75]
				4[50]
Потребности

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

2. Подсчитаем число занятых клеток таблицы, их 6, а должно быть m + n - 1 = 6. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 7*5 + 3*60 + 5*35 + 1*75 + 2*75 + 4*50 = 815

Этап II. Улучшение опорного плана.

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

u₁ + v₂ = 7; 0 + v₂ = 7; v₂ = 7

u₂ + v₂ = 2; 7 + u₂ = 2; u₂ = -5

u₂ + v₁ = 1; -5 + v₁ = 1; v₁ = 6

u₁ + v₃ = 3; 0 + v₃ = 3; v₃ = 3

u₁ + v₄ = 5; 0 + v₄ = 5; v₄ = 5

u₃ + v₄ = 4; 5 + u₃ = 4; u₃ = -1

	v1=6	v2=7	v3=3	v4=5
u1=0		7[5]	3[60]	5[35]
u2=-5	1[75]	2[75]
u3=-1				4[50]

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_i > c_ij

(3;1): -1 + 6 > 3; ∆₃₁ = -1 + 6 - 3 = 2

Выбираем максимальную оценку свободной клетки (3;1): 3

Для этого в перспективную клетку (3;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

					Запасы
		7[5][-]	3[60]	5[35][+]
	1[75][-]	2[75][+]
	3[+]			4[50][-]
Потребности

Цикл приведен в таблице (3,1; 3,4; 1,4; 1,2; 2,2; 2,1;). Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 2) = 5. Прибавляем 5 к объемам грузов, стоящих в плюсовых клетках и вычитаем 5 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план.

					Запасы
			3[60]	5[40]
	1[70]	2[80]
	3[5]			4[45]
Потребности

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

u₁ + v₃ = 3; 0 + v₃ = 3; v₃ = 3

u₁ + v₄ = 5; 0 + v₄ = 5; v₄ = 5

u₃ + v₄ = 4; 5 + u₃ = 4; u₃ = -1

u₃ + v₁ = 3; -1 + v₁ = 3; v₁ = 4

u₂ + v₁ = 1; 4 + u₂ = 1; u₂ = -3

u₂ + v₂ = 2; -3 + v₂ = 2; v₂ = 5

	v1=4	v2=5	v3=3	v4=5
u1=0			3[60]	5[40]
u2=-3	1[70]	2[80]
u3=-1	3[5]			4[45]

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_i <= c_ij. Минимальные затраты составят: F(x) = 3*60 + 5*40 + 1*70 + 2*80 + 3*5 + 4*45 = 805

Проверим оптимальность найденного плана по первой теореме двойственности (в оптимальном решении значения целевых функций прямой и двойственных задач совпадают: F = G). G = 0*100 -3*150 -1*50 + 4*75 + 5*80 + 3*60 + 5*85 = 805

Анализ оптимального плана.

Из 1-го склада необходимо груз направить в 3-й магазин (60), в 4-й магазин (40). Из 2-го склада необходимо груз направить в 1-й магазин (70), в 2-й магазин (80). Из 3-го склада необходимо груз направить в 1-й магазин (5), в 4-й магазин (45)

ЗАДАНИЕ 4

Решить задачу о назначении венгерским методом по известной матрице эффективностей.

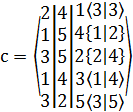
Решение:

Поскольку не указано, будем решать задачу на минимум (стандартная постановка). Решение будем искать венгерским методом.

Составляем исходную таблицу (матрицу):

Этап 1. В каждой строке ищем минимальный элемент (выделяем жирным в таблице) и отнимаем от всех элементов строки. Получим:

Теперь проводим аналогичную процедуру для всех столбцов: ищем наименьший элемент по столбцу и отнимаем его из всех элементов столбца. Получим:

Задачей является распределение всех подлежащих назначению единиц в клетки с нулевой стоимостью.

Этап 2. Выбираем строку с одним нулем (строка №1), выделяем нуль жирным и зачеркиваем (выделено серым) оставшиеся нулевые значения этого столбца (столбца №3). Выбираем строку с одним нулевым значением (строка №5), выделяем нуль. Выбираем строку с одним нулем (строка №3), выделяем нуль жирным и зачеркиваем (выделено серым) оставшиеся нулевые значения этого столбца (столбца №4). Выбираем строку с одним нулем (строка №4), выделяем нуль жирным и зачеркиваем (выделено серым) оставшиеся нулевые значения этого столбца (столбца №1).

Выбираем строку с одним нулевым значением (строка №2), выделяем нуль.

Получаем оптимальную матрицу назначений

Минимальное значение целевой функции: 1 +2+2+1 +2=8.

ЗАДАНИЕ 5

Решить задачу по теме «Элементы теории массового обслуживания».

Какому условию должны удовлетворять интенсивности х =8 и 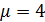для одноканальной СМО с отказами, чтобы вероятность обслуживания составляла 0,5?

Решение:

Системы массового обслуживания.

Исчисляем показатели обслуживания для одноканальной СМО:

Интенсивность потока обслуживания:

Интенсивность нагрузки.

ρ = λ*t_обс = 8 * 0.5 = 4

Интенсивность нагрузки ρ=4 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.

Вероятность, что канал свободен (доля времени простоя канала).

Следовательно, 20% в течение часа канал будет не занят, время простоя равно t_пр = 12 мин.

Доля заявок, получивших отказ.

p₁ = 1 - p₀ = 1 - 0.2 = 0.8

Значит, 80% из числа поступивших заявок не принимаются к обслуживанию.

Относительная пропускная способность.

Доля обслуживаемых заявок, поступающих в единицу времени:

Q = p₀ = 0.2

Абсолютная пропускная способность.

A = Q * λ = 0.2 * 8 = 1.6 заявок/мин.

Среднее время простоя СМО.

t_пр = p_отк * t_обс = 0.8* 0.5 = 0.4 мин.

Среднее число обслуживаемых заявок.

L_обс = ρ * Q = 4 * 0.2 = 0.8 ед.

Число заявок, получивших отказ в течение мин: λ * p₁ = 6 заявок в мин.

Номинальная производительность СМО: 1 / 0.5 = 2 заявок в мин.

Фактическая производительность СМО: 1.6 / 2 = 80% от номинальной производительности.

ЗАДАНИЕ 6

Найти решение матричных игр.

Решение:

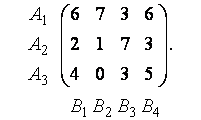
Предварительно упростим матричную игру, опустив излишние стратегии. Поскольку элементы первой строки платёжной матрицы не меньше соответствующих элементов третьей строки, в паре стратегий 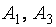игрока А стратегия является доминирующей, а стратегия 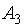− доминируемой, поэтому опустим последнюю, вычеркнув из платёжной матрицы третью строку:

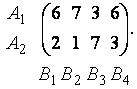
В этой платёжной матрице элементы первого столбца не больше соответствующих элементов четвёртого столбца, поэтому в паре стратегий 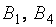игрока В стратегия 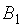является доминирующей, а стратегия 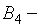доминируемой; опустим излишнюю стратегию 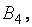вычеркнув из последней платёжной матрицы четвёртый столбец:

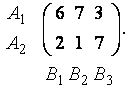
Дальнейшее упрощение матричной игры невозможно.

Пользуясь табл. 1.1, сведём игру к паре симметричных взаимо­двойственных задач линейного программирования (табл. 1.2)

Таблица 1.2

Игрок А	Игрок В

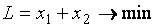
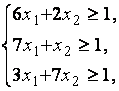
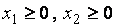
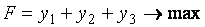
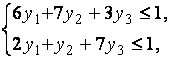
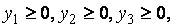
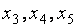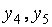Приведём обе задачи к каноническому виду, вводя дополнительно в системы ограничений прямой и двойственной задач неотрицательные балансовые неизвестные и соответственно:

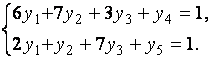
В прямой и двойственной задачах базис усматривается сразу: для задачи минимизации − 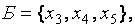для задачи максимизации − 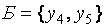. Следует отметить, что задача минимизации не имеет предпочтительного вида в базисе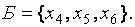

Установим соответствие неизвестных прямой и двойственной задач (рис. 1.1).

Дата добавления: 2015-04-24