Базисные неизвестные Свободные неизвестные

Свободные неизвестные Базисные неизвестные

Рис. 1.1. Соответствие неизвестных прямой и двойственной задач

Поскольку задача максимизации в базисе 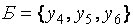имеет предпочтительный вид, составим для неё начальную симплекс-таблицу (табл. 13.3), добавив дополнительную строку неизвестных задачи максимизации, учитывая установленное соответствие.

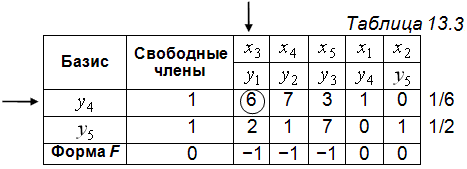
Реализацию алгоритма симплекс-метода для табл. 13.3 (и последующих симплекс-таблиц 13.4 и 13.5) оставим без комментариев

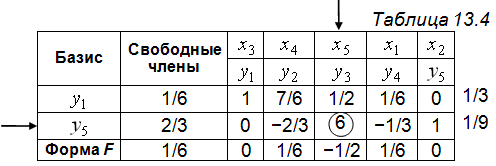
Таблица 1.5

Базис	Свободные члены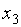
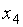
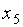
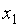
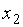
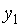
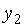
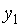
	1/9		11/9		7/36	−1/12
	1/9		−1/9		−1/18	1/6
Форма F	2/9		1/9		5/36	1/12

Оптимальное решение задачи максимизации, записанной в канонической форме, имеет вид:

Оптимальное решение этой задачи найдено в базисе 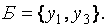Следовательно, двойственная ей задача минимизации имеет оптимальное решение в базисе Оптимальное решение задачи минимизации запишем по последней строке таблицы 13.5:

Исключая балансовые переменные, получим оптимальные решения прямой и двойственной задач:

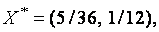
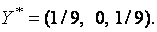
Соответствующее оптимальное значение целевых функций:

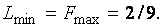
Тогда цена матричной игры

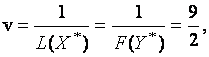
оптимальная смешанная стратегия первого игрока (игрока A) имеет вид

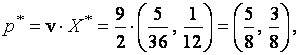
оптимальная смешанная стратегия второго игрока (игрока B) имеет вид:

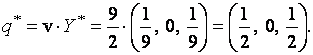
Поскольку данная матричная игра была упрощена путём удаления заведомо невыгодных стратеги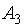й и 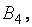её окончательное решение имеет вид:

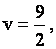
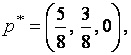
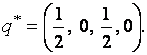
ЗАДАНИЕ 7

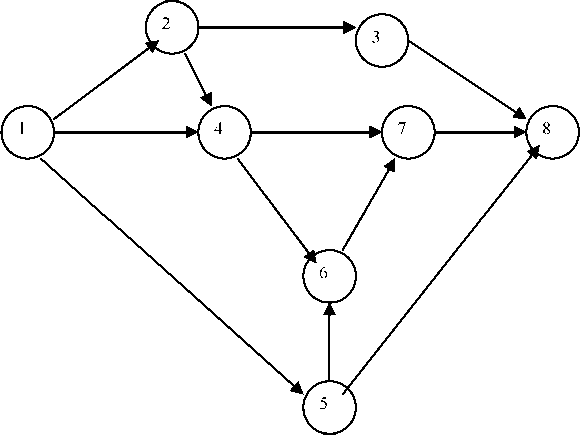
Решить задачу по теме «Сетевое планирование». Для заданной сетевой модели некоторого комплекса работ определить время и критический путь.

Решение:

Коды работ	Длительность работ (дни)
1-2
2-3
3-8
1-4
4-6
4-7
6-7
7-8
1-5
5-8
2-4
5-6

Рассмотрим прямой ход. Пусть Tj означает минимальное время окончания всех работ, конец которых изображается вершиной с номером j. Очевидно, T₁ =0, далее последовательно находим

^Tj = ^{max (T}i + j ^j = ^2,N^,

где i - номер вершин сетевого графика, из которых выходят векторы, входящие в вершину с номером j; t_ij - длительность работ с началом в вершине i и концом в вершине j, N - количество вершин сетевого графика. При j=N получаем минимальное время графика T^=T_N.Tj являются ранними сроками начала (окончания) работ, конец (начало) которых изображается вершиной j. Итак,

T^p = 0,

T2 = max(Ti^p + t₁₂) = 7,

T₃^p = max(T₂^p + 1 ₂₃) = 8,

T₄^p = max(T^p + 1₁₄, T^p + 1 ₂₄) = max(8,7) = 8,

T₅^p = max(T₁ ^p +1₁₅) = 4,

T₆^p = max(T₅^p + 1 ₅₆, T₄^p + 1 ₄₆) = max(4,16) = 16,

T₇^p = max(T₄^p + 1 ₄₇, T₆^p +1 ₆₇) = max(17,21) = 21,

T₈^p = max(T₃^p + 1 ₃₈, T₇^p +1 ₇₈, T₅^p +1 ₅₈) = max(12,24,16) = 24.

Тогда Ткр = 24 - минимальное время графика.

Рассмотрим обратный ход. Пусть T_iⁿ означает наибольшее время окончания всех работ, входящих в вершину i, Ткр=Т^.

Ti = min (Tjⁿ - -_ц), i = N2,

где j - номер вершины, к которой направлены векторы, выходящие из вершины с номером i.

T₈ⁿ = 24,

^T7 = min(^T₈ⁿ - 1 ₇₈) = ²1,

^T6 = ^min(T7^{n - t} ₆7⁾ = ^16,

T₅ⁿ = min(T₈ⁿ -1₅₈, T₆ⁿ - t_S6) = min(12,16) = 12,

T₄ⁿ = min(T₇ⁿ - 1 ₄₇, T₆ⁿ -1 ₄₆) = min(12,8) = 8,

T₃ⁿ = min(T₈ⁿ -1₃₈) = 20,

T₂ⁿ = min(T₃ⁿ - 1 ₂₃, T₄ⁿ -1₂₄) = min(19,8) = 8,

T" = min(T₂ⁿ -1₁₂, T₄ⁿ -1₁₄, T₅ⁿ -1₁₅) = min(1,0,8) = 0.

T_iⁿ - поздние сроки начала (окончания) работ, начало которых изображается вершиной i.

Для определения критического пути составим таблицу.

Работа	Продолжит.	Ранние сроки	Поздние сроки	Полный Резерв	Свободн. Резерв
(ij)	tii	Ti^p	Ti^p	Ti^n	Ti^n	Rii	^rii
1,2
2,3
3,8
1,4
4,6
4,7
6,7
7,8
1,5
5,8
2,4
5,6

Здесь R_H = Tn -? -1.., r= Tf - T^p - t _H, - полный и свободный резерв. Критический путь сетевого графика составляют работы, для которых R _ij =r _ij Получаем путь (1,4)-(4,6)-(6,7)-(7,8), время - 24 дня.

Дата добавления: 2015-04-24