П.2. Логические операции над предикатами

Предикаты, так же, как высказывания, принимают два значения и и л (1, 0), поэтому к ним применимы все операции логики высказываний.

Рассмотрим применение операций логики высказыва­ний к предикатам на примерах одноместных предикатов.

Пусть на некотором множестве М определены два предиката Р (х) и Q (х).

Определение 4. Конъюнкцией двух предикатов Р (х) и Q (х) называется новый предикат Р (х)& Q (х), который принимает значение «истина» при тех и только тех значениях 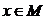, при которых каждый из предикатов Р (х) и Q (х) принимает значение «истина» и принимает значение «ложь» во всех остальных случаях. Очевидно, что областью истинности предиката Р (х)& Q (х) является общая часть областей истинности предикатов Р (х) и Q (х), т.е. пересечение .

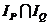Так, например, для предикатов Р (х): «х – четное число» и Q (х): «х кратно 3» конъюнкцией Р (х)& Q (х) является предикат «х – четное число и х кратно 3», то есть предикат «х делится на 6».

Определение 5. Дизъюнкцией двух предикатов Р (х) и Q (х) называется новый предикат 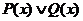, который принимает значение «ложь» при тех и только тех значе­ниях 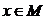, при которых каждый из предикатов при­нимает значение «ложь» и принимает значение «исти­на» во всех остальных случаях. Ясно, что областью истинности предиката 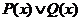является объединение областей истинности предикатов Р (х) и Q (х), то есть объединение .

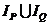Определение 6. Отрицанием предиката Р (х) назы­вается новый предикат 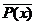, который принимает значе­ние «истина» при всех значениях 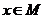, при которых предикат Р (х) принимает значение «ложь», и принима­ет значение «ложь» при тех значениях 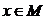, при кото­рых предикат Р (х) принимает значение «истина». Очевидно, что, .

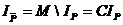Определение 7. Импликацией предикатов Р (х) и Q (х) называется новый предикат 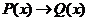, который является ложным при тех и только тех значениях 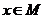, при которых одновременно Р (х) принимает значение «истина», а Q (х) – значение «ложь» и принимает значе­ние «истина» во всех остальных случаях.

Так как при каждом фиксированном 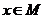справедлива равносильность 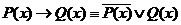, то .

Ясно, что при выполнении логических операций над предикатами к ним применимы и равносильности алгеб­ры логики.

Пример 3. Пусть даны предикаты А (х,у) и В (х,у), определенные на множестве 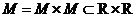. Най­ти множество истинности предиката 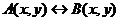и изобразить ее с помощью кругов Эйлера-Венна.

Решение. Так как 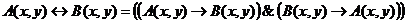, то .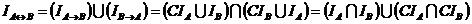

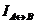изображена серой частью рисунка:

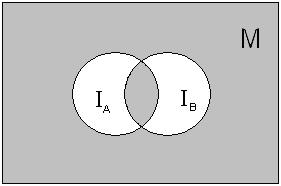
Можно рассматривать и обратную задачу: «Зная об­ласть истинности предиката, полученного в результате применения логических операций к некоторым преди­катам, записать этот предикат».

Пример 4. Записать предикат, полученный в результате логических операций над предикатами Р (х), Q (х) и R (х), область истинности которого изображена серой частью рисунка:

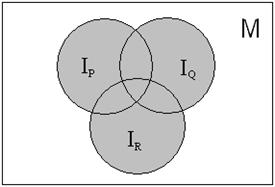
Решение. Так как здесь 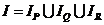, то искомый предикат имеет вид: .

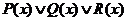Дата добавления: 2015-04-24