
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
III.Исследование функций с помощью производной
|
|
|
|
II. Дифференциальное исчислениефункции одной переменной.
ПЕРЕЧЕНЬ ПРИМЕРНЫХ ЗАДАЧ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
I. Введение в анализ: множества, функция. Предел и непрерывность функции одной переменной
1. Найти область определения функции:
а) 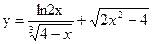 ;
;
б) 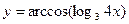 .
.
2. Построить график функции y = |x| + |x2 - 9|.
3. Найти точки разрыва функции
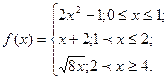
4. Вычислить:
а) 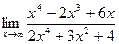 ; б)
; б) 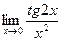 ;
;
в) 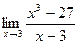 ; г)
; г) 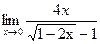 ;
;
д) 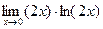 ; е)
; е) 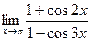 ;
;
ж) 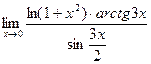 ; з)
; з) 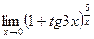 .
.
5. Записать уравнения касательной и нормали к графику функции:
а) 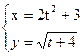 в точке t = 5;
в точке t = 5;
б) 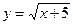 в точке x = 4.
в точке x = 4.
6. Найти производные второго порядка от функций:
а) y2 + xy = 0;
б) 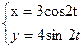 .
.
7. Найти асимптоты графика функции:
а) 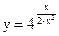 ; б)
; б) 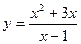 .
.
8. Найти дифференциал функции:
а) 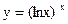 ; б)
; б) 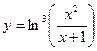 .
.
9.Используя понятие дифференциала, вычислить:
а) 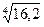 ; б) е0,97; в) ln(e + 0,03).
; б) е0,97; в) ln(e + 0,03).
11.Для функции спроса 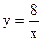 в зависимости от цены x найти эластичность спроса y по цене в точке x = 4.
в зависимости от цены x найти эластичность спроса y по цене в точке x = 4.
12.Найти экстремумы функции 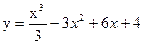 .
.
13.Исследовать возрастание и убывание функции y = 2x3 + 18x2 – 42x.
14.Найти точки перегиба функции y = x4 + 6x2 – 8.
15.Найти наибольшее и наименьшее значения функции y = 4x3 – 6x – 3 на [0; 3].
IV.Неопределённый интеграл.
18. Найти интегралы методом интегрирования по частям:
a) 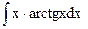 ;
;
b) 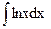 ;
;
c) 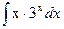 ;
;
d) 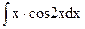 ;
;
e) 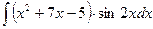 .
.
19. Найти интегралы, используя подходящую подстановку:
a) 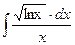 ; b)
; b) 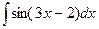 ;
;
c) 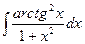 ; d)
; d) 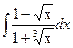 ;
;
e) 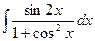 ; f)
; f) 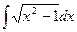 ;
;
g) 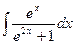 ; h)
; h) 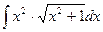 .
.
20. Найти интегралы от рациональных функций:
a) 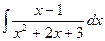 ;
;
b) 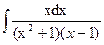 ;
;
c) 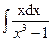 .
.
21. Найти интегралы от тригонометрических функций:
a) 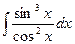 ; b)
; b) 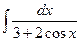 ;
;
c) 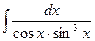 ; d)
; d) 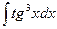 .
.
V.Определённый интеграл.
22. Вычислить определенные интегралы:
a) 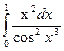 ; d)
; d) 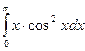 ;
;
b) 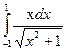 ; e)
; e) 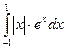 .
.
c) 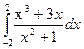 ;
;
23. Зависимость производительности q от времени t задается функцией q(t). Найти количество продукта Q, производимого за время a ≤ t ≤ b.
23.1. q(t) = 80+ 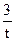 , a = 5, b = 10;
, a = 5, b = 10;
23.2. q(t) = 10+ 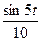 , a = 0, b = 12.
, a = 0, b = 12.
24. Найти среднюю производительность qср за время a ≤ t ≤ b, если производительность q зависит от времени t по закону:
a) q(t) = 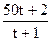 , 0 ≤ t ≤ 10;
, 0 ≤ t ≤ 10;
b)q(t) =arctgt, 5 ≤ t ≤ 10;
c)q(t) =5+ 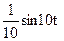 , 0 ≤ t ≤ 10π.
, 0 ≤ t ≤ 10π.
25. Количество электроэнергии q, потребляемое за единицу времени, зависит от времени t. Сколько электроэнергии потребляется за время a ≤ t ≤ b, если:
a) q(t) =100+10sin 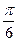 t+5sin
t+5sin 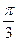 t, 9 ≤ t ≤ 20; b)q(t) =
t, 9 ≤ t ≤ 20; b)q(t) = 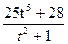 , 5 ≤ t ≤ 10.
, 5 ≤ t ≤ 10.
26. Затраты предприятия на содержание управленческого аппарата определяются функцией f(t)= 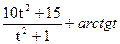 . Какими будут затраты за время 6 ≤ t ≤ 12?
. Какими будут затраты за время 6 ≤ t ≤ 12?
27. Вычислить площадь фигуры, ограниченной кривыми:
a)y = x2-6x+5, y = 0;b)y = x2+1, y = x+3.
28. Вычислить объем тела, полученного вращением вокруг оси Ox криволинейной трапеции, ограниченной линиями
a) x2-y2=a2, x=±2a; b) 2y2=x3, x=4.
29. Вычислить несобственные интегралы.
29.1. 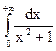 ; 29.4.
; 29.4. 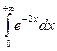 ;
;
29.2. 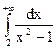 ; 29.5.
; 29.5. 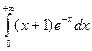 ;
;
29.3. 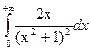 ; 29.6.
; 29.6. 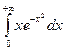 .
.
31. Исследовать сходимость:
31.1. 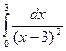 ; 31.4.
; 31.4. 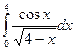 ;
;
31.2. 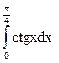 ; 31.5.
; 31.5.  .
.
31.3. 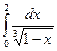 ;
;
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1208; Нарушение авторских прав?; Мы поможем в написании вашей работы!