Простейший поток событий как математическая модель

ЭКОНОМИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ФОРМУЛЫ НЬЮТОНА – ЛЕЙБНИЦА

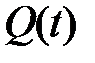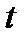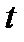Если – объём продукции, выпускаемый неким производителем за время , то производительность в момент времени будет: 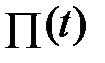= 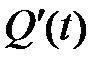. При таком толковании производной интеграл 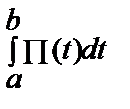численно равен объему продукции, выпушенной за время от 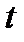= 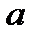до 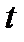= 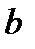, но этот же объем равен 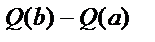, а потому 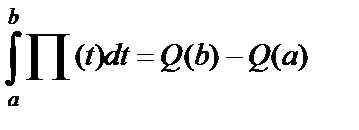, а это и есть формула Ньютона – Лейбница, так как 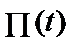– первообразная для .

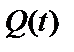Теперь отвлечёмся от конкретного содержания подынтегральных функций и их первообразных и запишем формулу Ньютона – Лейбница вообще для функции и её первообразной ):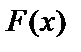

.

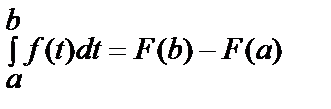Различные интерпретации формулы Ньютона – Лейбница показывают, что она математически выражает глубокие связи, существующие в объективной действительности, и таким образом является математической моделью всех таких связей.

При изучении случайных событий, т. е. таких, которые в результате опыта могут произойти или не произойти, мы будем идеализировать реальность и пользоваться математической моделью опыта и его исходов. Например, в модельном опыте при бросании монеты может выпасть герб или цифра, тогда как в реальных условиях монета может стать на ребро (событие 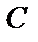). Конечно, в идеализированной модели событием 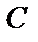мы пренебрегаем, как весьма маловероятным и потому несущественным. В такой модели при однократном подбрасывании монеты возможны два события: выпадение либо герба, либо цифры.

При построении вероятностных моделей широко используется принцип практической невозможности маловероятных событий или, что по существу то же самое, принцип практической достоверности событий, вероятность которых весьма близка к 1: если вероятность некоторого события 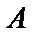в данном опыте весьма мала, то можно быть практически уверенным в том, что при однократном выполнении опыта событие 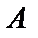не произойдёт.

В простейших вероятностных (статистических) моделях результаты исследований можно представить таблицей, в верхней строке которой указаны всевозможные несовместные элементарные исходы опыта, а в нижней – их вероятности (относительные частоты). Например, такая таблица, соответствующая однородной симметричной игральной кости, будет иметь вид:

События	А1	А2	А3	А4	А5	А6
Вероятности

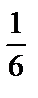
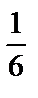
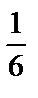
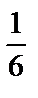
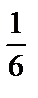
где 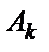событие – выпадение игральной кости, верхняя грань которой имеет номер .Сумма вероятностей, находящихся во второй строке таких таблиц, равна 1.

12) 2. СТАНДАРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ КАК МАТЕМАТИЧЕСКАЯ МОДЕЛЬ.

Название «математическое программирование» связано с тем, что целью решения задач, рассматриваемых в этой дисциплине, является математически обоснованный выбор программы действий (не путать с программированием – составлением программы для ЭВМ).

В математическое программирование обычно включаются задачи на максимум и минимум с ограничениями типа равенств или неравенств.

К линейному программированию относятся те задачи математического программирования, в которых и целевая функция, и ограничения линейны.

Если же целевая функция или хотя бы одно из ограничений нелинейно, то соответствующая задача является задачей нелинейного программирования. Простейшие задачи такого типа рассмотрены в пункте 7.1.

Из линейного программирования сначала рассмотрим задачу об использовании ресурсов.

Предприятие может осуществлять производство трех видов товара , , 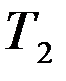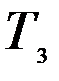из двух видов сырья 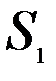и 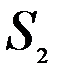. Нормы расхода на производство товаров вместе с данными о ценах и запасах представлены в таблице 7.1, где 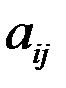– количество сырья 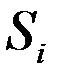, которое расходуется на производство единицы товара 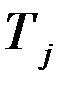, 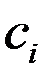– стоимость единицы товара 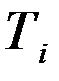. Требуется построить математическую модель для определения плана выпуска товаров 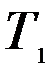, , 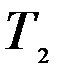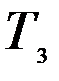в количествах , , 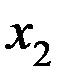, 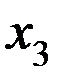при которых выручка от их реализации (продажи) была бы максимальной.

Математическая модель:

Найти значения 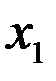, , 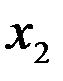, 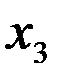которые доставляют 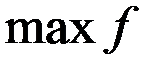, где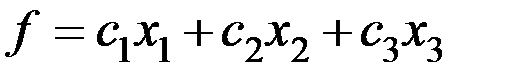

,

при условиях .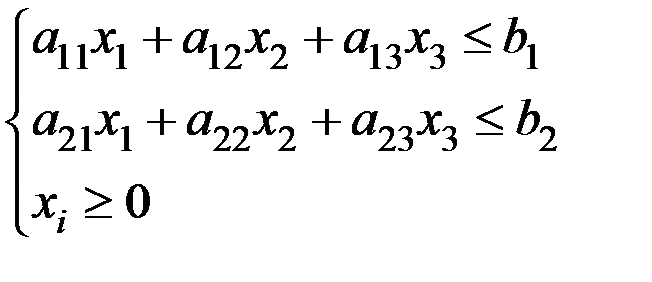

Этой системе неравенств должна удовлетворять совокупность всех вариантов производства, обеспеченных имеющимися ресурсами. (Задача линейного программирования, в которой ограничения на запасы записаны в виде неравенств).

Таблица 7.1

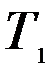
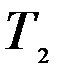
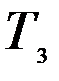
Виды товаров Виды сырья				Запасы
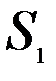
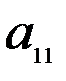
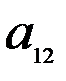
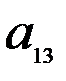
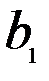
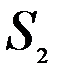
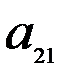
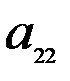
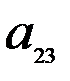
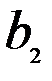
Цена единицы товара

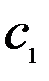
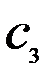
Теперь построим математическую модель транспортной задачи:

стоимость перевозки 1 т груза из пункта отправления 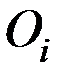в каждый пункт назначения 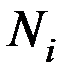задана таблицей 7.2.

Таблица 7.2

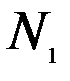
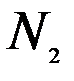
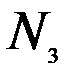
Пункты назначения   Пункты отправления				Запасы
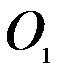
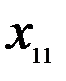
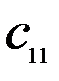
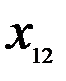
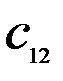
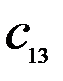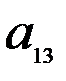
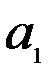
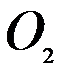
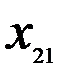
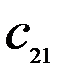
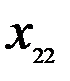
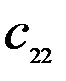
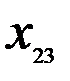
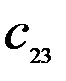
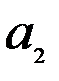
Потребность в грузе

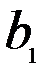
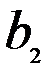
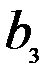
Здесь 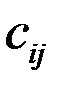– стоимость перевозки 1 т груза из пункта отправления 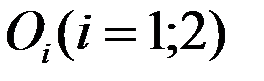в пункт назначения 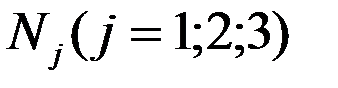. Весь груз из пунктов отправления нужно перевезти в пункты назначения, поэтому .

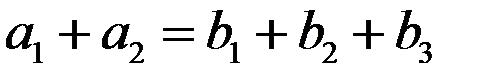Составить математическую модель для определения оптимального плана перевозки грузов так, чтобы общая стоимость транспортных расходов была бы наименьшей.

Обозначим через 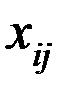– количество груза, предназначенного к отправлению из 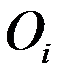в 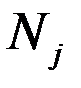, тогда придем к следующей математической модели: Найти значения 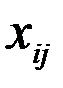, которые доставляют 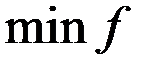, где 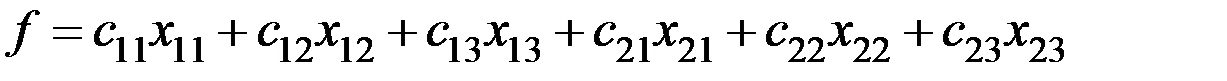, при условиях:

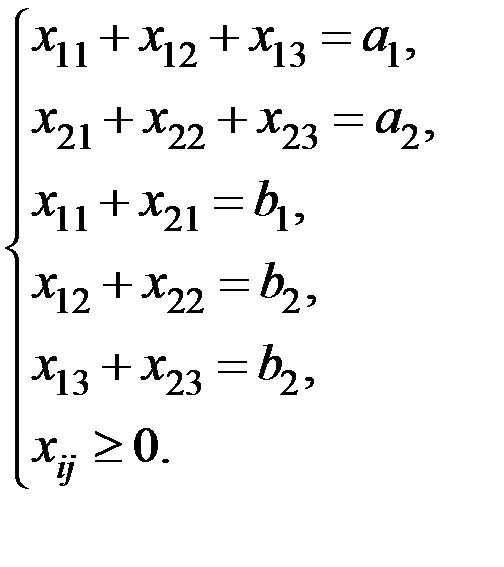
(Каноническая задача линейного программирования, в которой ограничения на запасы и потребности записаны в виде уравнений).

Дата добавления: 2015-04-24