Сущность вычислительного эксперимента. Математическая модель как основа его проведения

МЕХАНИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ФОРМУЛЫ НЬЮТОНА - ЛЕЙБНИЦА.

Задача об определении пути по известной зависимости скорости v (t) >0 от времени.

В этих условиях путь, пройденный точкой по траектории за промежуток времени от 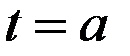до равен 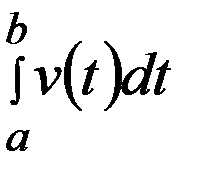(механический смысл определённого интеграла). Но этот же путь можно выразить и с помощью функции 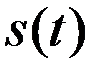: 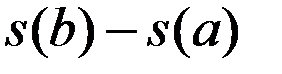, поэтому , а это и есть формула Ньютона – Лейбница, так как , т.е. 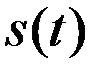– первообразная для .

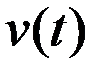Пример процесса колебаний подрессоренной массы

m – величина подрессоренной массы (кгс²/м),

р – сопротивление амортизатора (кгс/м),

c – жёсткость упругого элемента (кг/м).

z – вертикальная координата движения подрессоренной массы,

q₀ – амплитуда,

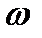- частота возмущающего воздействия дороги, принятого синусоидальным,

t – время.

Наше время характеризуется широким внедрением компьютеров во все сферы человеческой деятельности. С их появлением при решении многих задач используется метод, называемый вычислительным экспериментом.

В простейших случаях он сводится к вычислениям, связанным с перебором всех возможных вариантов из некоторого допустимого множества, отбрасыванию тех, которые не удовлетворяют условиям задачи.

При изучении какого-либо процесса математическими методами, прежде всего, строится его математическая модель. Изменяя в ней параметры, можно оценить влияние различных факторов на поведение процесса, т. е. получить такую же богатую информацию, как и при натурных испытаниях. По существу такая работа очень близка к эксперименту, только роль экспериментальной установки выполняет ЭВМ, а вместо реального процесса исследуется его математическая модель. Именно поэтому изучение реального, физического процесса таким способом в рамках принятой модели называют вычислительным (численным) или математическим экспериментом.

Одно из его достоинств состоит в том, что он дешевле, проще и безопаснее натурного. В вычислительном эксперименте можно моделировать условия, которые еще невозможно создать в лаборатории. Конечно, вычислительный эксперимент тесно связан с натурным, поскольку математическая модель процесса строится на основе закономерностей, выявленных из опыта, она должна хорошо отражать определенные стороны физического процесса. Вычислительный и натурный эксперименты дополняют друг друга и позволяют получать новые результаты.

Дата добавления: 2015-04-24