Преобразование моделей

Задача об определении площади криволинейной трапеции

ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА КАК МАТЕМАТИЧЕСКАЯ МОДЕЛЬ.

Рассмотрим задачи из разных областей знания, связанные между собой единством математической модели.

Так называют плоскую фигуру (рисунок 12.1), ограниченную графиком непрерывной на отрезке 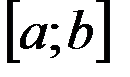функции 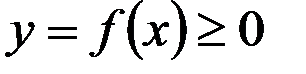, отрезком 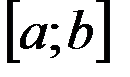и прямым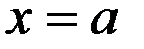и и 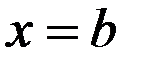. При определении её площади, буем исходить из простейшей фигуры – прямоугольника, площадь которого легко вычисляется. Для решения задачи разобьём отрезок 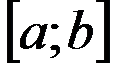на 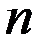равных частичных отрезков точками 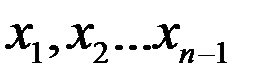, и положим для общности , 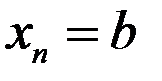(рисунок 12.1) и на каждом из них построим прямоугольник с высотой, равной ординате в середине частичного отрезка: 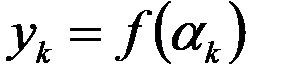, 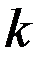– номер частичного отрезка. Поэтому площадь

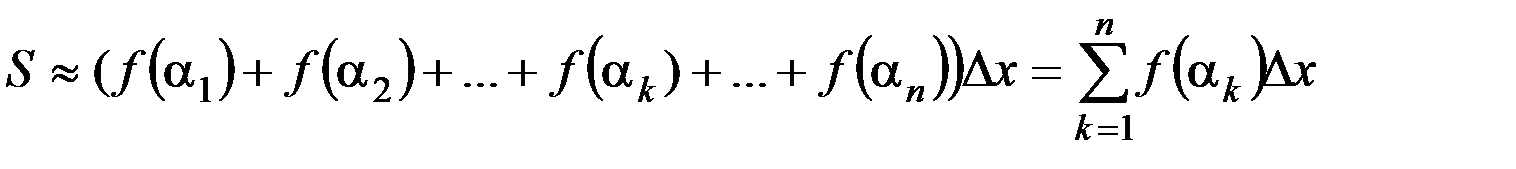(12.1)

где

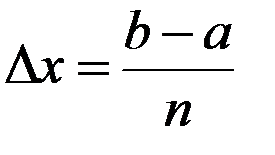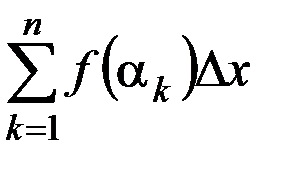, – интегральная сумма.

При

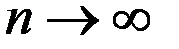, S =

(геометрический смысл определённого интеграла). Формула (12.1) может быть применена и для приближённого вычисления площади криволинейной трапеции и определённого интеграла.

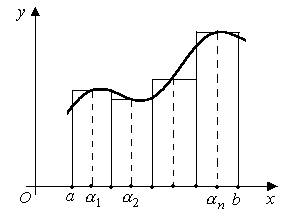
Рисунок 12.1 – Криволинейная трапеция

2. Задача об определении пути по известной зависимости скорости v (t) >0 от времени.

В этих условиях путь, пройденный точкой по траектории за промежуток времени от 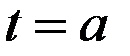до равен 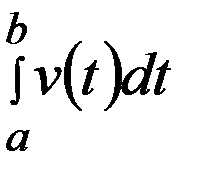(механический смысл определённого интеграла). Но этот же путь можно выразить и с помощью функции 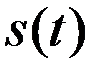: 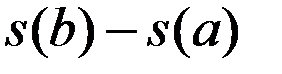, поэтому , а это и есть формула Ньютона – Лейбница, так как , т.е. 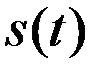– первообразная для .

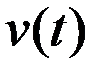Если 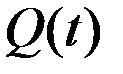– объём продукции, выпускаемый неким производителем за время , то производительность 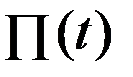в момент времени будет: 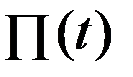= 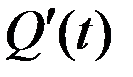. При таком толковании производной интеграл 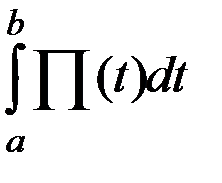численно равен объему продукции, выпушенной за время от = до = 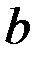, но этот же объем равен 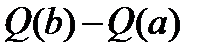, а потому 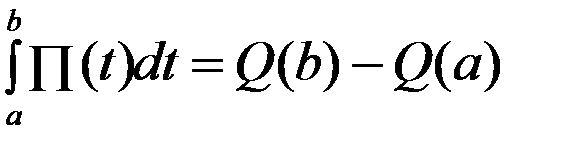, а это и есть формула Ньютона – Лейбница, так как 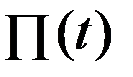– первообразная для .

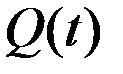Теперь отвлечёмся от конкретного содержания подынтегральных функций и их первообразных и запишем формулу Ньютона – Лейбница вообще для функции 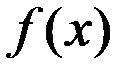и её первообразной ):

.

Различные интерпретации формулы Ньютона – Лейбница можно долго продолжать. Но и уже рассмотренные показывают, что она математически выражает глубокие связи, существующие в объективной действительности, и таким образом является математической моделью всех таких связей.

Дата добавления: 2015-04-24