Рассмотрим физическое подобие

В случае геометрического подобия изучение натуры при помощи ее модели довольно простое: отношение длин сходственных отрезков постоянно, площади подобных фигур пропорциональны квадратам длин их сходственных линий, объемы подобных тел, а также объемы любых соответственных их частей пропорциональны кубам длин их сходственных линий.

В современной теории подобия достаточные признаки подобия формулируются с помощью безразмерных комплексов величин, представляющих собой произведение степеней этих величин называемых критериями подобия. Рассмотрим этот вопрос в связи с геометрическим подобием фигур. Для этого заметим, что всякий объект может быть задан однозначно определяющими его параметрами. Например, круг однозначно определяется радиусом, треугольник тремя сторонами, двумя сторонами и углом между ними и т. п. Еще раз подчеркнем, что в подобных фигурах отношения длин соответствующих (сходственных) линейных элементов не изменяются! Именно эта неизменность отношений жестко связана с постоянством углов между соответствующими отрезками подобных фигур, что позволяет измерять углы отвлеченными числами, равными отношениям длин линейных элементов тех фигур, которым принадлежат углы.

Итак, построим угол с вершиной в точке О (рисунок 9.3) и проведем две любые дуги разного радиуса от одной стороны этого угла до другой. Так как оба образовавшиеся секторы подобны, то отношение длины дуги к длине соответствующего радиуса будет одинаковым и постоянным для данного угла. Это значит, что указанное отношение, т.е. число, однозначно определяет величину угла. Следовательно, этим числом можно измерять его величину. Такая мера угла, как известно, называется радианной.

Из рисунка 9.3 имеем: .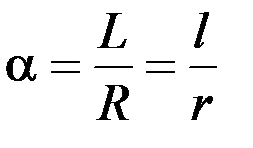

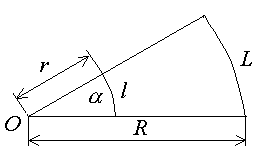
Рисунок 9.3 – Радианная мера угла .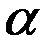

Рассмотрим треугольник, определяемый двумя сторонами и углом между ними (рисунок 9.4).

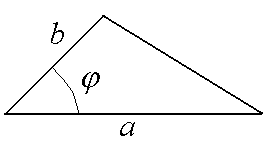
Рисунок 9.4 – Треугольник с определяющими параметрами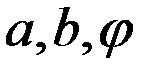

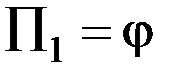безразмерная величина (число) – критерий подобия. Из двух величин «а» и «b», очевидно, можно составить только один независимый безразмерный комплекс (все другие могут через него выражаться, зависеть от него) 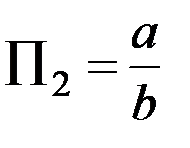. Теперь нетрудно установить, что если у двух треугольников критери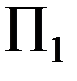и и 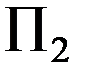– одинаковы, то они подобны. Действительно: пусть второй треугольник однозначно определяется параметрами Φ, А, В, тогда при 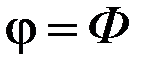, , 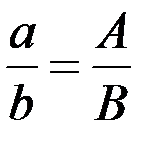т.е. 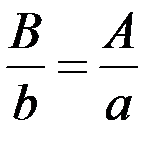, и следовательно, треугольники подобны.

Соответствующие признаки подобия треугольников и многоугольников могут быть переформулированы в терминах критериев подобия.

Подчеркнем, что при геометрическом подобии, длины элементов объектов, связанные с натурой, могут быть получены простым пересчетом соответствующих величин, относящихся к модели и наоборот.

Теперь введем понятие физически подобных объектов (систем, процессов и т.п.), как обобщение подобия геометрического. Два объекта называются физически подобными, если при заданных характеристиках одного можно получить соответствующие характеристики другого простым пересчетом, аналогичным пересчету при геометрическом подобии.

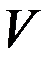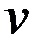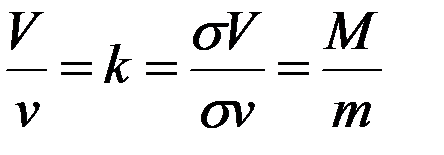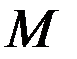Приведем пример. Для этого рассмотрим два геометрически подобных, однородных тела с одной и той же объемной плотностью , объемами и . Тогда , где и 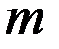– массы тел. Значит, 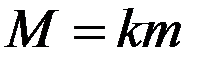, т.е. при заданной массе одного тела можно получить соответствующую массу 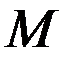другого простым пересчетом, аналогичным пересчету при геометрическом подобии. Значит, два тела физически подобны по массе.

Достаточным условием подобия двух объектов является равенство двух любых соответствующих критериев подобия, составленных из определяющих параметров, а так же начальных и граничных условий. Поэтому для того, чтобы создаваемый объект или имитируемое явление были подобны модели достаточно:

1) выбрать определяющие объект или явление величины и составить из них независимые критерии подобия;

2) выбрать параметры натуры так, чтобы ее критерии были такие же, как и у модели: 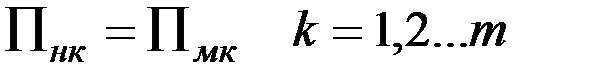, где 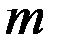– число всех независимых критериев подобия, при этом индекс м относится к модели, н – к натуре.

При исследовании подобных явлений большое значение имеет так называемая 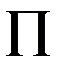(пи) - теорема. Функциональная зависимость между характеризующими объект или процесс величинами может быть представлена в виде зависимости между составленными из них критериями подобия:

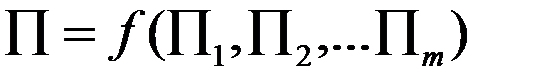. (9.1)

Вид зависимости (9.1) непосредственно следует из равенства (8.6), если в последнем обе части разделить на 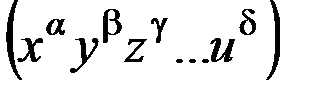и ввести для критерия 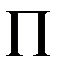обозначение .

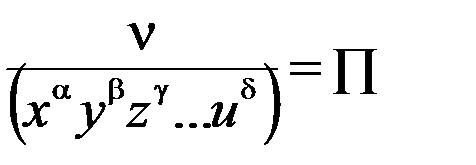Использование 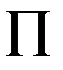– теоремы дает определенные преимущества при экспериментальном исследовании. Применяя безразмерные комплексы величин, полученные результаты можно распространить на все подобные явления, уменьшить число величин, которые следует связать функциональной зависимостью. Особенно легко находится эта зависимость, если критерий один (независимых от него, нет). Тогда функциональная зависимость имеет вид: 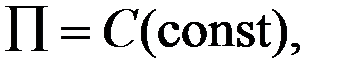т.е. в этом случае анализ размерностей позволяет получить полное решение задачи с точностью до постоянной, которая может быть найдена из эксперимента.

Так, длина окружности l определяется eе радиусом 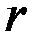и из двух этих величин можно образовать только один безразмерный комплекс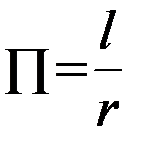 поэтому функциональная зависимость имеет вид

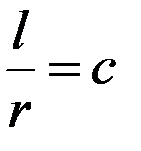; c, как показано выше, легко может быть определена экспериментально и 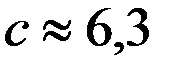(точно 2 ).

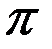Теперь определим период колебания математического маятника (рисунок 8.1).

Период Т будет однозначно определен, если задать g, l, 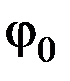и начальные условия при t =0, φ=φ ₀ и 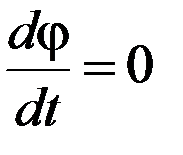. Таким образом, период колебаний маятника является функцией Т = F(g,l,φ₀) (силами сопротивления пренебрегаем). Простые преобразования, приведенные в п.8.3, показывают, что

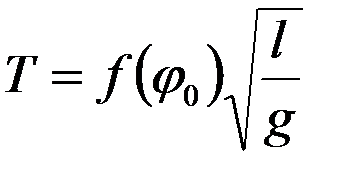, (9.2)

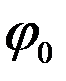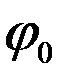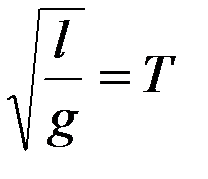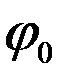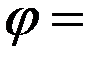
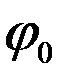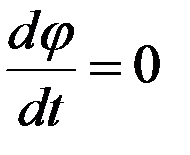где - единственный определяющий критерий подобия, так как только этим критерием определяется выражение f () , т.е. период колебаний. В формуле (9.2) критерий является определяющим, других определяющих критериев нет. Поэтому, если и при 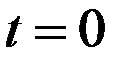для модели и натуры, то колебания маятников подобны. Проверим это утверждение и непосредственно. Пусть l_м, Т_м – длина и период маятника модели, а

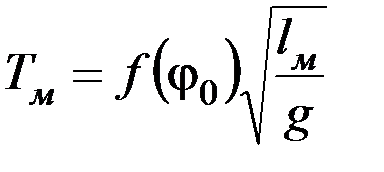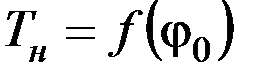
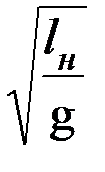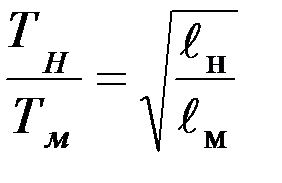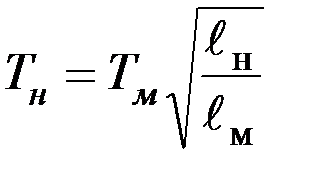l_н,Т_н – для натуры, тогда на основании (9.2) имеем и . Откуда и , или 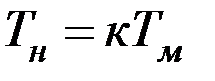, где коэффициент подобия 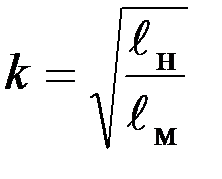, т. е. если мы найдем на основе эксперимента Т_м для модели и измерим l_м и l_н, то легко получим Т_н для натуры. Итак, 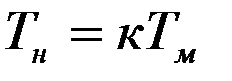, т. е. при заданном периоде Т_м одного маятника получаем соответствующий период Т_н другого простым пересчетом, аналогичным пересчету при геометрическом подобии.

Для малых колебаний справедлива формула (8.8)

T=с ₁ ,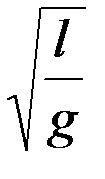

где с ₁ – постоянная, которую найдем из опыта.

Возьмем маятник длиной l =1 (м) и экспериментально определим его период. С помощью секундомера находим, что этот маятник за 10с совершает 5 колебаний. Поэтому Т =2c. Таким образом

2= c ₁ ,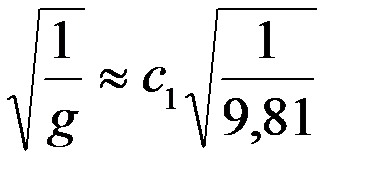

т.е. c ₁=6,27, тогда как теоретически 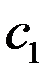= 2 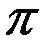. Отсюда Т 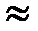6,27 .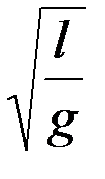

При малых 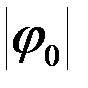и l_м =1м мы нашли на основе опыта Т_м =2 с. Пусть l_н =0,49 м тогда 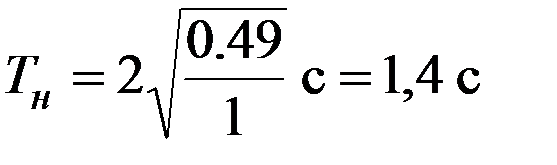. Сравним этот результат с экспериментальным, взяв маятник длины 0,49 м, тогда обнаружим, что он совершает 10 колебаний за 14 с, т.е. Т =1,4 с. Таким образом, пересчет соответствует эксперименту.

Дата добавления: 2015-04-24