
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математическая модель апории «ахиллес и черепаха» и ее разрешение
|
|
|
|
Определение суммы ряда
Для этого рассмотрим полоску бумаги 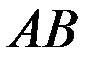 длиной 1 (дм) и шириной 1 (см) (рисунок 11.1)
длиной 1 (дм) и шириной 1 (см) (рисунок 11.1)
A C1 C2 C3 B
C1 C2 C3
Рисунок 11.1 – Модель полоски бумаги
Мысленно разрежем (или сложим) её пополам по отрезку 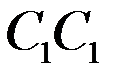 , затем разрежем (или сложим) правую часть
, затем разрежем (или сложим) правую часть 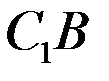 пополам по отрезку
пополам по отрезку 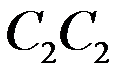 и т. д. до бесконечности. Тогда
и т. д. до бесконечности. Тогда  ;
; 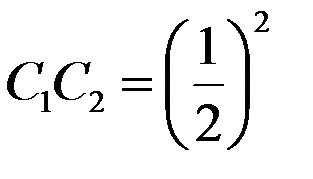 ;
; 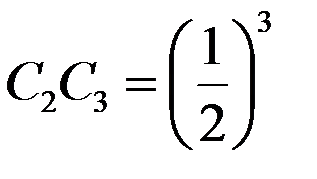 ; …
; … 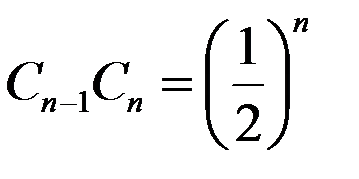 .
.
Теперь очевидно, что  (11.2)
(11.2)
и левая часть равенства (11.2), представляющая сумму бесконечного числа слагаемых, не только имеет смысл, но и равна 1, т. е. длине всей полоски. Но как найти сумму, находящуюся в левой части равенства (11.2), не зная заранее, что она равна 1.
Для этого сначала рассмотрим сумму первых n слагаемых
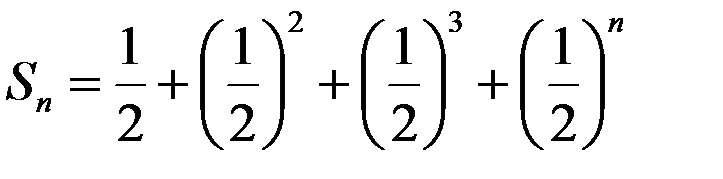 ,
,
представляющую для геометрической прогрессии сумму n её первых членов, которая в общем случае равна
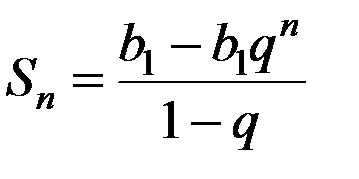 , (11.3)
, (11.3)
где 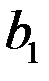 – первый член геометрической прогрессии, знаменатель которой
– первый член геометрической прогрессии, знаменатель которой  ≠ 1.
≠ 1.
Теперь определим бесконечную сумму, состоящую из членов геометрической прогрессии при 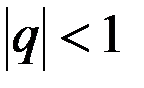 . Из (11.3) следует, что
. Из (11.3) следует, что
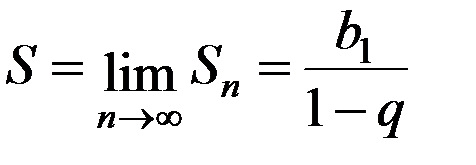 . (11.4)
. (11.4)
Так как в случае полоски длины 1, 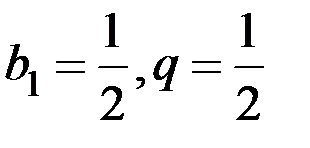 , то на основании (11.4)
, то на основании (11.4) 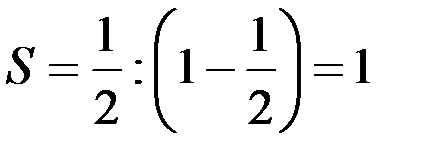 , что совпадает с (11.2). Итак, сумма членов бесконечной геометрической прогрессии при
, что совпадает с (11.2). Итак, сумма членов бесконечной геометрической прогрессии при 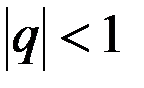 вычисляется по формуле (11.4).
вычисляется по формуле (11.4).
Отметим, что великий русский писатель Л. Н. Толстой на первой странице третьей части третьего тома романа «Война и мир» приводит описание другой апории Зенона «Ахиллес и черепаха»:
«Для человеческого ума непонятна абсолютная непрерывность движения. Человеку становятся понятны законы какого бы то ни было движения только тогда, когда он рассматривает произвольно взятые единицы этого движения. Но вместе с тем из этого - то произвольного деления непрерывного движения на прерывные единицы проистекает большая часть человеческих заблуждений. Известен так называемый софизм древних, состоящий в том, что Ахиллес никогда не догонит впереди идущую черепаху, несмотря на то, что Ахиллес идёт в десять раз скорее черепахи: как только Ахиллес пройдёт пространство, отделяющее его от черепахи, черепаха пройдёт впереди его одну десятую этого пространства; Ахиллес пройдёт эту десятую, черепаха пройдёт одну сотую и т. д. до бесконечности. Задача эта представлялась древним неразрешимой. Бессмысленность решения (что Ахиллес никогда не догонит черепаху) вытекала из того только, что произвольно были допущены прерывные единицы движения, тогда как движения и Ахиллеса и черепахи совершались непрерывно. Принимая всё более и более мелкие единицы движения, мы только приближаемся к решению вопроса, но никогда не достигаем его. Только допустив бесконечно – малую величину и восходящую от неё прогрессию до одной десятой и взяв сумму этой геометрической прогрессии, мы достигаем решения вопроса». Таким образом, и эта апория разрешается математически существованием суммы бесконечной прогрессии при  (в общем случае при
(в общем случае при 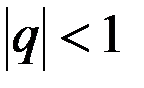 ) в формуле (11.4).
) в формуле (11.4).
19) 2. МЕТОД ПОДОБИЯ И ЕГО ПРИЛОЖЕНИЕ К ПОСТРОЕНИЮ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Рассмотрим следующие виды подобий:
1) геометрическое подобие: две геометрические фигуры подобны, если отношения длин всех соответственных элементов одинаковы.
2) физическое подобие: два объекта называются физически подобными, если при заданных характеристиках одного можно получить соответствующие характеристики другого простым пересчетом, аналогичным пересчету при геометрическом подобии.
По-видимому, на практике исторически первым применялось математическое моделирование, основанное на принципе подобия алгебраически описываемом пропорцией, представляющей равенство двух отношений или с функциональной точки зрения – функцией 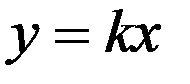 .
.
Для получения необходимых экспериментальных данных с целью определения величин, входящих в пропорцию или коэффициента 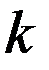 в линейную функцию используются удобные для исследования масштабы.
в линейную функцию используются удобные для исследования масштабы.
Рассмотрим геометрическое подобие:
Пусть, например, требуется определить высоту треугольной в плане башни, не производя непосредственно измерение высоты (рисунок 1). Если имеется фотоснимок башни, то, используя условие подобия можно довольно просто получить результат.
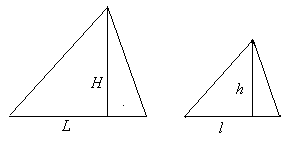
Рисунок 1 – Подобие объектов
Измерив легкодоступный размер 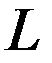 на натуре и размеры
на натуре и размеры 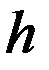 и
и 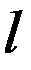 на модели (фотоснимке) на основании подобия, составим пропорцию
на модели (фотоснимке) на основании подобия, составим пропорцию 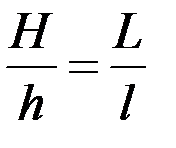 и найдем:
и найдем:  .
.
Такой подход всегда применим, если известно, что соответствующие фигуры подобны. В этой связи отметим, что точнее было бы говорить о подобии математических моделей объектов, так как сами объекты могут обладать и некоторыми особенностями, не включенными в модель.

Рисунок 9.2 – подобие кругов
 – длина окружности радиуса
– длина окружности радиуса 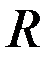 ,
, 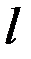 – длина окружности радиуса
– длина окружности радиуса 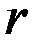
Поскольку все окружности (круги) подобны, то, рассмотрев рисунок 9.2, можно написать равенство
 или
или  (
(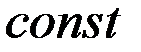 ) и, следовательно,
) и, следовательно, 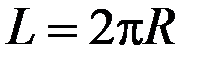 . Постоянное число
. Постоянное число  можно определить из эксперимента с любым круговым диском (моделью). Так, взяв и измерив длины его диаметра и граничной окружности, легко оценим
можно определить из эксперимента с любым круговым диском (моделью). Так, взяв и измерив длины его диаметра и граничной окружности, легко оценим  .
.
Установим также формулу площади круга. Так как все круги подобны, то из того же рисунка на основании теоремы о том, что площади подобных фигур относятся как квадраты сходственных отрезков, следует:
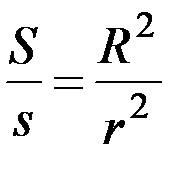 или
или 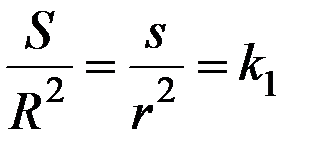 , где
, где  – константа. Поэтому
– константа. Поэтому 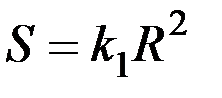 .
.
Учитывая, что все круги подобны, приходим к выводу, что  – величина постоянная:
– величина постоянная: 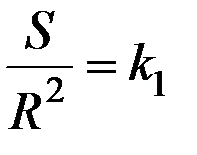 и может быть приближенно определена экспериментально, например, взвешиваниями круга и единичного квадрата, вырезанных из однородного тонкого картона. При этом получается:
и может быть приближенно определена экспериментально, например, взвешиваниями круга и единичного квадрата, вырезанных из однородного тонкого картона. При этом получается: 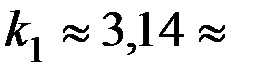
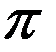 . Итак,
. Итак, 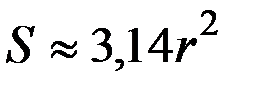 .
.
Поскольку объемы пространственных подобных фигур относятся как кубы сходственных отрезков, то для двух шаров, большие круги которых указаны на рисунке 9.2, имеем:
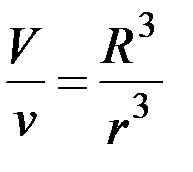 или
или 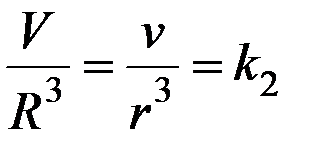 , где
, где 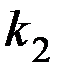 – константа.
– константа.
Поэтому 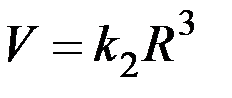 , т.е.
, т.е.  и
и 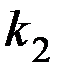 может быть, как указано выше, определено экспериментально, погрузив полностью шарик от подшипника в мерный сосуд с водой:
может быть, как указано выше, определено экспериментально, погрузив полностью шарик от подшипника в мерный сосуд с водой: 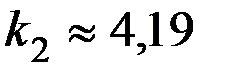 , точно
, точно 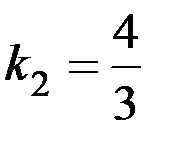
 .
.
Отметим, что площади сферических поверхностей относятся как квадраты их радиусов и потому 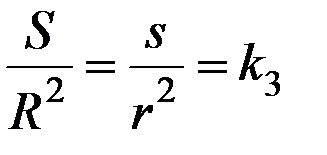 , где
, где 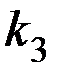 –константа. Следовательно,
–константа. Следовательно, 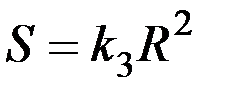 , причем
, причем 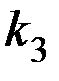 нетрудно выразить через
нетрудно выразить через  .
.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1180; Нарушение авторских прав?; Мы поможем в написании вашей работы!