Оценки истинного значения измеряемой величины

Пусть производится n независимых равноточных измерений некоторой физической величины, истинное значение a, которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины 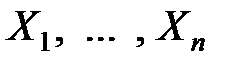. Эти величины независимы, имеют одно и то же математическое ожидание a, распределены нормально. Значит, истинное значение измеряемой величины можно оценить по I и II.

Пример. По данным 9 независимых равноточных измерений физической величины среднее арифметическое 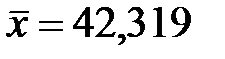и 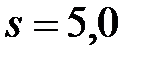. Оценить истинное значение измеряемой величины с надежностью 0,95.

Решение: по II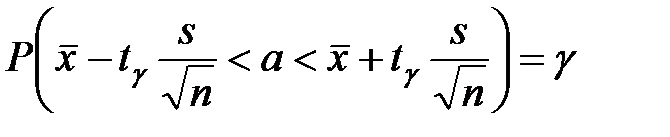

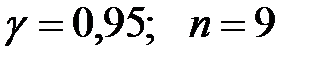, значит, .

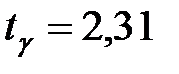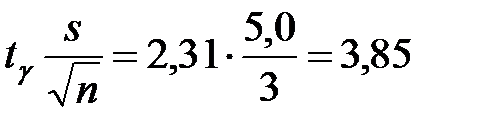, значит,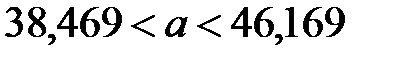

Коэффициент корреляции. Линии регрессии.

Разберемся с этими понятиями на примере. Пусть даны следующие выборки – урожайность земель некоторого сельскохозяйственного предприятия и количество внесенных удобрений на каждый квадратный метр разных по урожайности участков земли. Решение этой задачи крайне важно для руководителей предприятия, ибо известно, что как недовнесение удобрений, так и излишнее удобрение может дать отрицательный эффект. Ясно, что таблица урожайности разных участков земли и таблица внесенных удобрений на эти участки связаны между собой. Если установить эту зависимость, можно оптимальным для урожая способом удобрять те, или иные участки.

Математическая постановка этой и близких к ней задач требует, установить, имеется ли связь между заданными таблицами (коррелируют ли данные таблиц, или таковой связи не наблюдается)? Если связь между табличными данными есть, как записать ее в виде формулы?

Пусть известны 10 значений каждой переменной

k
X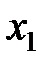
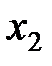
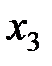
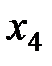
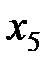
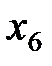
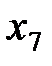
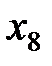
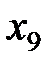
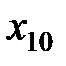
Y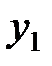

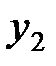
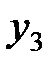
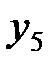
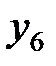
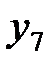
Обозначим ,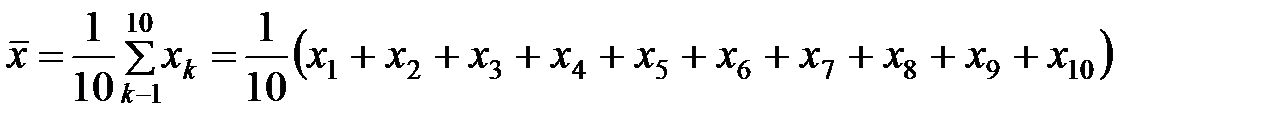

,

.

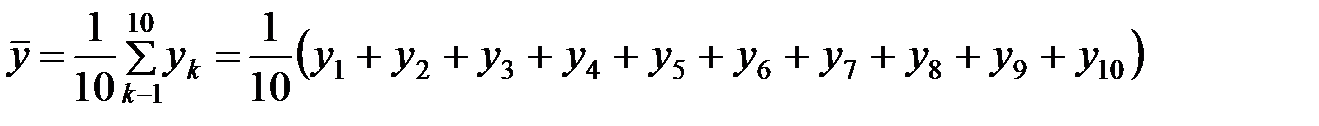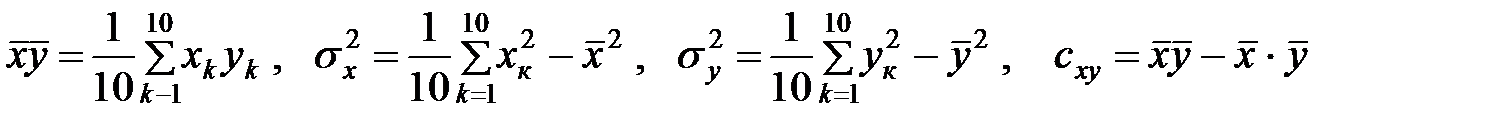Коэффициент корреляции определяется формулой

.

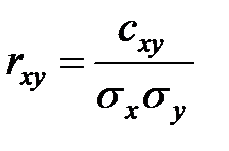Известно, что этот коэффициент равен нулю, если табличные данные для X и Y не коррелируют, то есть не зависят друг от друга. Если 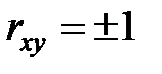, то зависимость между этими данными линейная.

Если выполняется неравенство 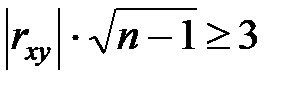, где n – объем выборки, то связь между X и Y вероятна.

Когда в ходе наблюдения за объектом определяются пары чисел , причем некоторые пары могут быть одинаковыми, но каждому значению x соответствует единственное значение y, линии линейной регрессии определяются уравнениями

,

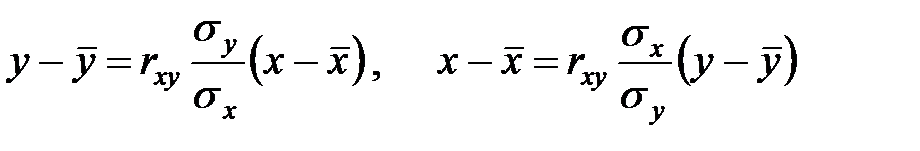Причем одна из линий регрессии дает линейное приближение y от x (регрессия Y на X), другая – x от y (регрессия X на Y).

Прямые различны, поскольку первая прямая получается в результате решения задачи о минимизации суммы квадратов отклонений случайной величины по вертикали, вторая - по горизонтали.

Применительно к задаче о связи урожайности с количеством внесенных удобрений, одна из линий регрессии позволяет оценить, при каком

Если в ходе наблюдений установлено, что одному значению x соответствует несколько значений y, или одному значению y соответствует несколько значений x, уравнения регрессии видоизменяются:

.

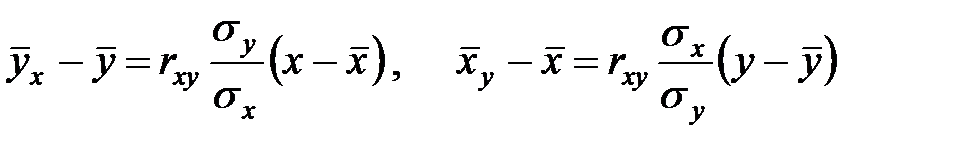Здесь 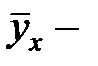среднее значение случайной величины y при одном значении x, 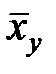- среднее значение случайной величины x при одном значении y.

Дата добавления: 2015-04-24