Вопрос 35

Пусть 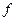определена в некоторой окрестности точки 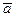, и пусть в этой точке существуют , .

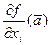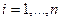Определение. Линейная функция от 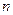независимых переменных 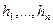вида

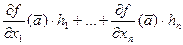(20.1)

называется дифференциалом 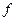в точке 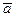и обозначается .

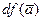Каждую из независимых переменных 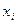, 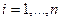можно рассматривать как функцию 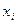, причем 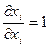, , 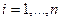а для любого 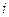и любого 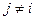имеем .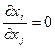

Тогда, последовательно выбирая 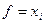, 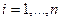и применяя равенство (20.1), получаем

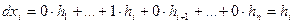. (20.2)

Подставляя в (20.1) вместо 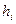величину 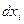согласно (20.2), получаем более часто употребляемую запись дифференциала:

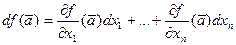. (20.3)

Обычно величинам переменных 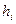придают значения 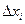приращений независимых переменных, не входящих при добавлении 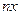к рассматриваемой точке за границу рассматриваемой области. Независимость переменных 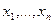означает, что если взять какое-то приращение 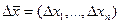, то оно не меняется при переходе от одной точки области к другой (а для зависимых переменных переход к другой точке вызывает соответствующие изменения вектора ).

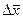Поэтому выражение (20.3) можно заменить на

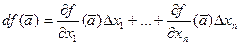(20.4)

для независимых переменных 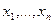(для них, напомним еще раз, ).

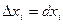Вспомним (см. вопрос 18) определение дифференцируемой функции: ее приращение имело вид

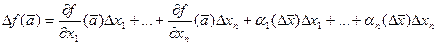, (20.5)

где 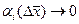при .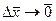

Согласно (20.4), равенство (20.5) можно переписать в виде

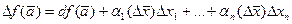. (20.6)

Оно означает, что если среди чисел 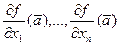есть отличное от нуля, то 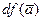представляет собой главную, притом линейную по 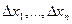, часть приращения.

Определим (пока формально) вектор 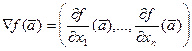. Тогда 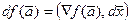(скалярное произведение). (Вектор градиента служит обобщением понятия производной функции. Напомним, что .)

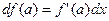Для отображения 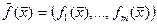пространства 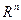в 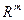, состоящего из дифференцируемых функций, также можно определить дифференциал 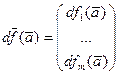. При этом

.

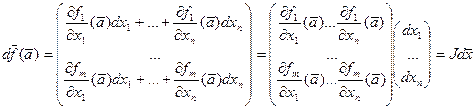Матрица 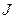называется матрицей Якоби отображения .

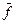(Свойства матрицы Якоби даны в приложении к этому билету, в конце его.)

Перейдем к вопросу о том, что будет в случае зависимых переменных .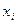

Производная сложной функции. Инвариантность формы первого дифференциала.

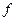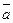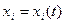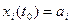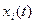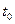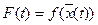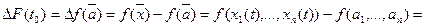
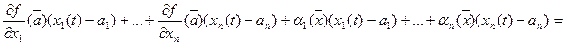
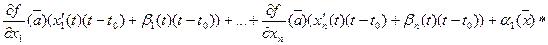
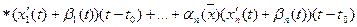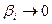Допустим, что дифференцируемая в точке функция, и , причем – дифференцируемые в точке функции. Положим . Тогда , где при .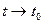

В определении дифференцируемости можно доопределить функции 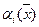в точке 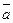, положив 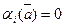. Тогда при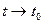 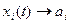(а может быть, и принимает значения 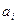). Но тогда 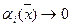(так как 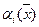у нас доопределены в точке 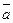нулем) и 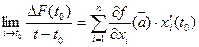, таким образом, 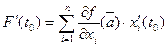(6)

Рассмотрим теперь случай, когда 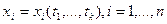. Применяя полученное выше правило, получим, в очевидных обозначениях 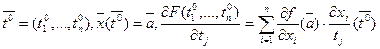(7)

Равенства (6) и (7) дают правила вычисления производных сложных функций.

Следствие. Следствием этих правил является инвариантность форм первого дифференциала. Именно, пусть 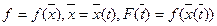. Тогда .

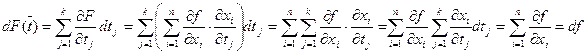Это означает, что как в случае независимых переменных 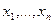, так и в случае зависимых переменных .

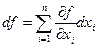Дата добавления: 2015-04-24