Примеры. Вопрос32.Функции и отображения

Вопрос32.Функции и отображения. Предел, непрерывность.

Определение 32.1 Функция сопоставляет элементам множества (называемого областью определения) числа .

Определение 32.2 Отображение сопоставляет элементам множества элементы .

Таким образом, функция – это частный случай отображения . Задать отображение – это все равно, что задать 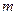функций

1. 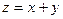- функция двух переменных, паре сопоставляет число .

2. Отображение

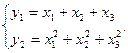
3. Вектор-функция 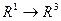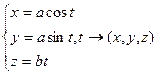Винтовая линия.

Пусть - предельная точка области определения .

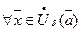
“Конкретизируя” окрестности, это определение в метрических пространствах , или, для

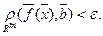Или

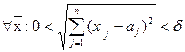выполняется неравенство

(17.1)

Теорема 32.1. .

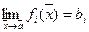Доказательство.

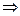Поскольку , из (17.1) следует, что при . Но это как раз и означает, что .

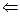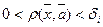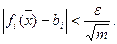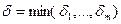. Пусть - фиксировано. Выберем так, чтобы при выполнялось неравенство Взяв получаем, что при 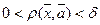выполняется неравенство

.

Определение 32.3. Отображение непрерывно в точке 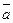, если

Согласно сказанному выше, непрерывность отображения равносильна непрерывности всех функций .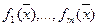

Так же, как и в случае функций одной переменной, справедлива следующая теорема.

Теорема 32.2. Если 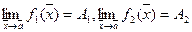, то 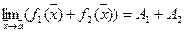, , 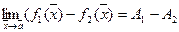и если 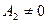, то .

Следствие. Сумма, разность, произведение и частное (при ) непрерывных функций и являются непрерывными функциями.

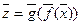Теорема 32.3. Если непрерывно в точке , отображение непрерывно в точке , то отображение непрерывно в точке .

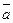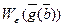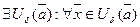
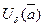Доказательство. Для всякой окрестности существует такая, что . Но . Эта окрестность - искомая, т.к. .

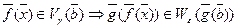Теорема 32.4. (Теорема о сохранении знака непрерывной функции). Если 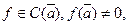то .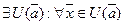

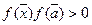Доказательство. Достаточно доказать, что если , то и 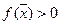. Действительно, взяв получаем по определению непрерывности окрестность такую что .

Теорема 32.5. Непрерывный образ компактного множества есть компактное множество. (без доказательства).

Замечание. Эта теорема непосредственно обобщает теоремы 1 семестра о том, что непрерывная на отрезке функция ограничена и достигает наибольшего и наименьшего значений.

Теорема 32.6. Непрерывный образ связного множества (т.е. множества, любые 2 точки которого можно соединить кривой, целиком лежащей внутри этого множества) есть связное множество. (без доказательства).

Замечание. Эта теорема обобщает теорему 1 семестра о том, что непрерывная на отрезке функция принимает все свои промежуточные значения.

Теорема 32.7. (Теорема Кантора). Непрерывная на компакте функция равномерно непрерывна на нем, т.е. .

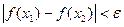Дата добавления: 2015-04-24