Точки перегиба

Теорема 30.3. Для того чтобы функция f, дважды дифференцируемая в интервале (a,b), была выпуклой вниз (вверх) на (a,b), необходимо и достаточно, чтобы во всех точках.

Выпуклость дважды дифференцируемой функции

◄ Согласно критерию монотонности функции на промежутке (теорема29.1), условие для всех является необходимым и достаточным условием возрастания (убывания) производной функции f’(x) на . Последнее свойство, согласно теореме 30.1 предыдущего пункта, является необходимым и достаточным условием выпуклости вниз (вверх) функции f на интервале .►

Определение 30.2. Точку кривой , называют точкой перегиба, если она отделяет участок кривой, где функция выпукла вверх, от участка кривой, где функция выпукла вниз.

Если функция дифференцируема на интервале , то по теореме 30.1 в некоторой окрестности абсциссы точки перегиба её производная либо возрастает слева от точки , а справа от неё убывает, либо - наоборот. В первом случае рассматриваемая точка будет точкой максимума производной f’(x), во втором случае – точкой минимума. Если предположить существование 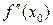, то по теореме 23.1 (Ферма), применённой к функции f’(x), получим: 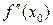=0.

Это условие играет такую же роль в отношении точек перегиба, какую играло условие в отношении точек экстремума, т.е. оно является необходимым, но не достаточным. Действительно, функция , очевидно, выпукла вниз, но её вторая производная, равная 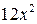, обращается в ноль при .

Достаточное условие точки перегиба даёт следующее правило, вытекающее из теоремы 30.3:

Дата добавления: 2015-04-24