
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выпуклость графика функции
|
|
|
|
Пусть 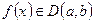 Тогда в каждой точке её графика есть касательная, уравнение которой:
Тогда в каждой точке её графика есть касательная, уравнение которой:

Определение. Функция 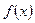 называется выпуклой вниз на (a,b), если
называется выпуклой вниз на (a,b), если 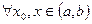
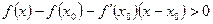 (т.е точка графика
(т.е точка графика  лежит над касательной к этому графику в любой точке
лежит над касательной к этому графику в любой точке 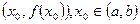 )
)
Выпуклость вверх определяется условием:
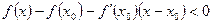
Теорема1. Если производная 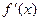 - возрастающая на (a,b) функция, то
- возрастающая на (a,b) функция, то  - выпуклая вниз на (a,b)
- выпуклая вниз на (a,b)
►  =
= 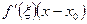 , где
, где 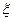 лежит между
лежит между  и x, по теореме Лагранжа, все условия которой, разумеется, выполнены.
и x, по теореме Лагранжа, все условия которой, разумеется, выполнены.
Пусть 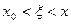 . Тогда
. Тогда  >0 и
>0 и  , поэтому
, поэтому  -
- 
Если же 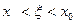 ., то
., то  <0,
<0,  и снова
и снова  -
-  ◄
◄
Аналогично доказывается, что если 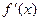 удовлетворяет на (a,b), то график
удовлетворяет на (a,b), то график  - выпуклая вверх функция.
- выпуклая вверх функция.
Примером служит функция полезности, полезность продукта с ростом насыщения падает, что означает выпуклость графика этой функции вверх.
Если  имеет вторую производную на (a,b), то из теоремы 1 следует:
имеет вторую производную на (a,b), то из теоремы 1 следует:
Если  >0 на (a,b), то график функции выпуклый вниз, если
>0 на (a,b), то график функции выпуклый вниз, если  <0 - то вверх.
<0 - то вверх.
В качестве примера рассмотрите  и
и 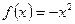
Точка, в которой направление выпуклости меняется на противоположное, называется точкой перегиба. Если существует  то, поскольку в точке перегиба
то, поскольку в точке перегиба  производная имеет экстремум, в ней вторая производная равна 0, т.е.
производная имеет экстремум, в ней вторая производная равна 0, т.е. 
Например,  имеет в
имеет в  =0 перегиб, так как слева от
=0 перегиб, так как слева от  =0 т.е при x<0,
=0 т.е при x<0,  <0, и при x>0,
<0, и при x>0,  >0.
>0.
В самой точке  =0
=0  =0
=0
Разумеется, равенство  - это необходимое условие точки перегиба. Оно не является достаточным, как показывает пример функции
- это необходимое условие точки перегиба. Оно не является достаточным, как показывает пример функции 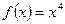 . Она имеет вторую производную
. Она имеет вторую производную  , которая не меняет знак, но обращается в 0 в точке
, которая не меняет знак, но обращается в 0 в точке  =0. Эта функция выпукла вниз на R.
=0. Эта функция выпукла вниз на R.
Достаточное условие точки перегиб даёт такое утверждение:
Пусть  непрерывны на (a.b) и пусть в точке
непрерывны на (a.b) и пусть в точке  выполнены условия:
выполнены условия: 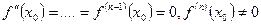 .
.
Тогда если n – нечётное число, то  - точка перегиба, если n – чётное число, то в
- точка перегиба, если n – чётное число, то в  нет перегиба.
нет перегиба.
Для доказательства используем формулу Тейлора с остаточным членом в форме Пеано:
 -
-  , где
, где  при
при 
Из условий следует, что
 -
- 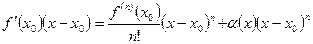
Рассуждая, как в случае вопроса о точках экстремума, получаем, что знак первой части совпадает со знаком  , если n – чётное число, и меняется, если n – нечётное число (при x из окрестности точки
, если n – чётное число, и меняется, если n – нечётное число (при x из окрестности точки  ) Это доказывает утверждение.
) Это доказывает утверждение.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 346; Нарушение авторских прав?; Мы поможем в написании вашей работы!