Фазные преобразования переменных

Математическая модель (3.26) для электрических процессов в синхронном двигателе получена для двухфазной модели машины. Электромеханический двигатель в ЭМУР имеет трехфазную обмотку статора, поэтому возникает необходимость преобразования переменных трехфазной машины к переменным двухфазной модели и наоборот. Основой для такого преобразования может служить физический смысл координатных преобразований. Один и тот же результирующий вектор магнитодвижущей силы может быть создан как двухфазной, так и трехфазной обмоткой, поэтому для получения формул двухфазно-трехфазных преобразований можно использовать тот же принцип, что и для получения формул координатных преобразований.

Итак, возникает задача преобразования реальных переменных статора трехфазной машины к ортогональной системе координат т.е. к реальным переменным статора эквивалентной двухфазной машины. Решение этой задачи существенно осложняется, в связи с необходимостью перехода от объекта с тремя фазами к обобщенной модели с двумя фазами, так как разница в числе фаз затрудняет выполнение условия инвариантности мощности. Учитывая это, представим реальные переменные трехфазной машины в виде векторов, и будем полагать, что преобразованные переменные в осях 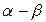не равны, а пропорциональны сумме проекций реальных переменных 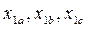на оси 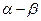. На основании построений, показанных на рис. 3.6а, можно записать

(3.27)

где 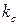— согласующий коэффициент пропорциональности, выбор которого должен осуществляться из условия инвариантности мощности.

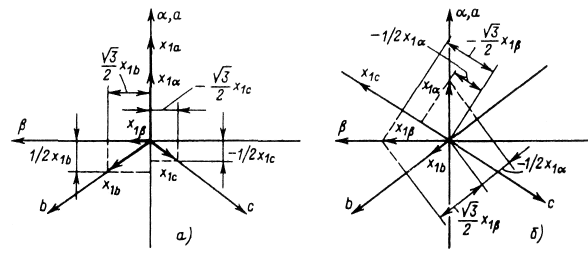
Рис. 3.6. Схемы преобразования переменных трехфазной машины

Рассмотрим случай, когда переменные трехфазной машины подчиняются условию

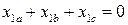. (3.28)

С учетом (3.28) уравнения (3.27) преобразуются к виду

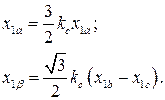(3.29)

Формулы обратного преобразования можно получить аналогично с помощью рис. 3.6б

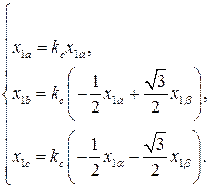(3.30)

При выполнении условия (3.28) третье уравнение системы (3.30) может быть получено с помощью первых двух, так как 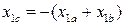. Для определения согласующего коэффициента 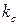, обеспечивающего выполнение условия инвариантности мощности при преобразовании переменных, выразим с помощью уравнения (3.28) суммарную мгновенную мощность, потребляемую обмотками статора трехфазной машины через переменные эквивалентной двухфазной машины

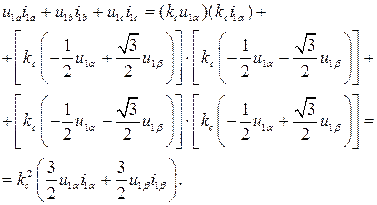
Следовательно, для выполнения условия инвариантности мощности согласующий коэффициент должен иметь значение

, (3.31)

при этом

.

В общем случае

,

и тогда приходится считаться с наличием переменных нулевой последовательности 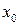. Поэтому формулы прямого и обратного преобразования для этих условий имеют вид

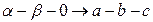
(3.31)

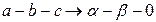
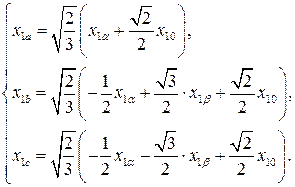(3.32)

Практически необходимость использования формул преобразования (3.31) и (3.32) возникает при строгом анализе несимметричных режимов работы симметричной трехфазной машины. При этом следует иметь в виду, что токи нулевой последовательности не влияют на момент, развиваемый двигателем, поэтому в большинстве случаев влияние переменных нулевой последовательности на динамику электромеханических систем может не учитываться.

Предполагая, что выполнено условие баланса (3.28), запишем преобразования (3.29) и (3.30) в матричной форме

· переход от 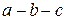к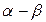

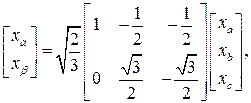(3.33)

· переход от 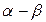к

(3.34)

В электромеханическом усилителе руля, обмотки двигателя соединены по схеме “звезда”, поэтому воспользуемся первым законом Кирхгоффа (3.28). Перепишем (3.28) в иной форме

. (3.34)

Подставив выражение (3.34) в (3.33), получим более упрощенную формулу перевода переменных из координат 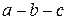в координаты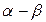

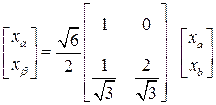. (3.35)

Уравнения (3.26) показывают, что наиболее простой вид уравнения токов и электромагнитного момента синхронного двигателя с постоянными магнитами имеют во вращающейся системе координат 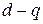, однако в реальных условиях токи и напряжения можно измерять и подавать только в неподвижной системе координат 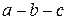. Поэтому необходимо определить преобразования, связывающие все системы координат 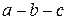, 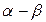и .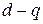

Матрица преобразований от 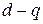к 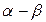легко находится из рис.2.4, если учесть условие (3.24). Имеем

. (3.36)

Матрица преобразований от 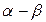к 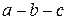получена выше, выражение (3.34)

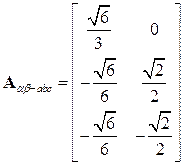. (3.37)

Из соотношений (3.36),(3.37) нетрудно найти матрицу перехода от 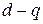к 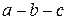. Имеем

. (3.38)

Обратные преобразования определяются простым транспонированием матриц прямого преобразования

. (3.39)

Формулы (3.36)–(3.39) будут использоваться в дальнейшем для составления полных моделей ЭМУР как в неподвижной системе координат 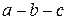, так и во вращающейся 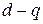, а также для преобразования переменных от одной системы координат к другой.

Дата добавления: 2015-04-24