Парный Т критерий Стьюдента

Сравнение двух зависимых групп

Критерий Краскела-Уоллиса

Критерий Краскела-Уоллиса - это непараметрическая альтернатива одномерному (межгрупповому) дисперсионному анализу. Он используется для сравнения трех или более выборок, и проверяет нулевые гипотезы, согласно которым различные выборки были взяты из одного и того же распределения, или из распределений с одинаковыми медианами. Таким образом, интерпретация критерия Краскела-Уоллиса в основном сходна с параметрическим одномерным дисперсионным анализом, за исключением того, что этот критерий основан скорее на рангах, чем на средних.

В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.

Вычисление значения t осуществляется по формуле:

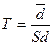
где d_i=x_i-y_i — разности между соответствующими значениями переменной X и переменной У, а d - среднее этих разностей;

Sd вычисляется по следующей формуле:

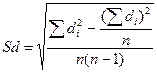
Число степеней свободы k определяется по формуле k=n-1. Рассмотрим пример использования t-критерия Стьюдента для связных и, очевидно, равных по численности выборок.

Если tэмп<tкрит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.

Изучался уровень ориентации учащихся на художественно-эстетические ценности. С целью активизации формирования этой ориентации в экспериментальной группе проводились беседы, выставки детских рисунков, были организованы посещения музеев и картинных галерей, проведены встречи с музыкантами, художниками и др. Закономерно встает вопрос: какова эффективность проведенной работы? С целью проверки эффективности этой работы до начала эксперимента и после давался тест.

	До эксперимента	После эксперимента	d	d^2
			-1
Сумма

d=63/10=6,3

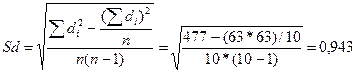
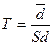=6,678

Число степеней свободы: k=10-1=9 и по таблице приложения находим tкрит =2.262, экспериментальное t=6,678, откуда следует возможность принятия альтернативной гипотезы (H₁) о достоверных различиях средних арифметических, т. е. делается вывод об эффективности экспериментального воздействия.

В терминах статистических гипотез полученный результат будет звучать так: на 5% уровне гипотеза Н₀ отклоняется и принимается гипотеза Н₁

Дата добавления: 2015-04-24