Построение итогового эллипса погрешностей в конечной точке

Построение эллипса погрешностей от счисления в конечной точке плавания

В связи с тем, что лаг и компас имеют свои случайные погрешности

s_DL= 2,4% s_ГК= 2,0°

в конце плавания возникают две векториальные погрешности:

вдоль линии пути

v_s = S_пл · s_DL = 54.1 · 0.024 = 1.30 м.м.,

поперек линии пути

v_К = S_пл · s_К / 57.3 = 54.1 · 2 / 57.3 = 1.89 м.м.

Поскольку эти векториальные погрешности всегда перпендикулярны, то они становятся полуосями эллипса погрешности от счисления места:

b = 1.30 м.м., a = 1.89 м.м.;

при этом нет никакой необходимости пользоваться Приложением №5 к МТ-75.

Для определения итогового эллипса погрешностей сложим векториальные погрешности, полученные при определении места судна по пеленгам с векториальными погрешностями счисления. Для этого выстроим ряд этих погрешностей с указанием их направлений:

v_p1 = v₁ = 0.87 м.м. y₁ = 15°

v_p2 = v₂ = 0.30 м.м. y₂ = 57°

v_K = v₃ = 1.89 м.м. y₃ = 35,9°

v_S = v₄ = 1.30 м.м. y₄ = 305.9°

Введем систему координат так, чтобы ось Х совпадала с направлением на N_и, а ось Y была перпендикулярна ей. Спроецируем векториальные погрешности на эти оси и найдем суммарные векториальные погрешности. Так как изначально векториальные погрешности не коррелированы, то сложить их можно, используя простое квадратическое сложение:

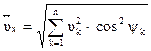= 1.73 м.м.

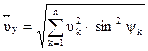= 1.57 м.м.

Поскольку мы проектировали на оси одни и те же векториальные погрешности, то между суммарными проекциями возникает зависимость, которую оценим коэффициентом корреляции. Определим корреляционный момент этих проекций:

= 2.73

Представим эти вычисления в развернутой форме в виде табл.2

Табл.2 Расчет параметров финального эллипса погрешностей

vk	yk	Х	Y	Х*Х	Y*Y	X*Y
0.87		0.84	0,225	0,706	0.051	0.189
0.30		0.163	0,252	0.027	0.064	0.041
1.89	35.9	1.53	1,11	1.69	1.232	1.698
1.30	305.9	0.762	1,05	0.581	1.103	0.800
S				3.004	2.45	2.728

Направление большой полуоси СКП – эллипса:

j =½* arctg [2M_xy/(v_x² - v_y²)] ± 90° =

½*arctg [5.46/0.554] ± 90° = 42.1° - 90° = -47.9

Полуоси эллипса находятся из системы уравнений:

a² + b² = = 3.004 + 2.45 = 5.45

a² – b² = 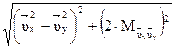= Ö[(0,554)² + (5.46)²] = 4.49,

откуда простым вычислением находим:

a = 2.23м.м.

b = 0.693 м.м.

Зная величины полуосей эллипса и направление его большой оси, легко построить сам эллипс погрешностей (рис.5).

1.10. «Размазывание» конечного стандартного эллипс в круг с вероятностью 95% накрытия им истинного места судна.

Вычисляем эксцентриситет эллипса

е = b /a = 0.693/2.23 = 0.31

По таблице 4,14 из МТ-2000 по величине e и надежности 95% находим R = 1.9

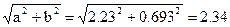М = м.м.

М_зад = М · R = 1.9 · 2.34 = 4.45 м.м.

Обратим ваше особое внимание на две приближенных формулы для оценки точности места судна, о которых часто спрашивают эксперты на Государственных квалификационных экзаменах, и которые вы точном варианте мы использовали выше.

1. Радиальная погрешность места судна для надежности накрытия 95 % при определении места по двум пеленгам:

М_зад = ,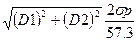

где D1,D2 – дистанции до ориентиров, sр – погрешность наблюдения пеленгов в градусах.

2. Радиальная погрешность места судна для надежности накрытия 95 % при определении места по двум дистанциям:

М_зад = 2Ö2*s_D,

где s_D – погрешность наблюдения дистанций до ориентиров.

Дата добавления: 2015-04-24