Пример выполнения лабораторной работы

Задание: для набора параметров

получить фазовые портреты, соответствующие различному поведению систем

·

·

·

·

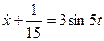
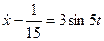
При данных параметрах получаем 4 колебательных системы.

Теоретический расчет:

Рассмотрим однородное (автономное) уравнение. Найдем его решение (1).

(1) 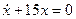- это ДУ с разделяющимися переменными.

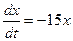
Общее решение автономного уравнения имеет вид:

Применим метод вариации произвольной постоянной:

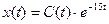
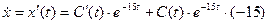
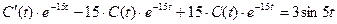
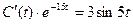
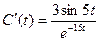
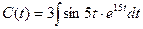- этот интеграл является циклическим интегралом (два раза интегрируем его по частям):

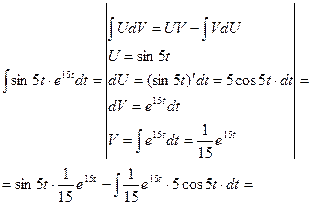
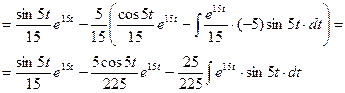
Введем переменную 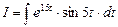, тогда:

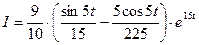
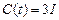
Подставим полученное C(t) в общее решение автономного уравнения:

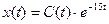
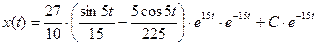
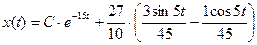- общее решение неавтономного уравнения.

После алгебраических и тригонометрических преобразований приведем решение к виду (9).

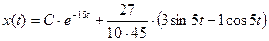
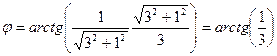
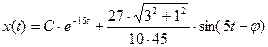
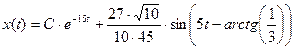
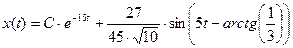
Компьютерное моделирование:

В Mathcad решение дифференциальных уравнений выполняется с помощью функции Odesolve. Эта функция требует записи вычислительного блока, состоящего из трех частей:

1. ключевого слова Given (Дано);

2. дифференциального уравнения и начальных или граничных условий к нему;функции оdesolve(x, xk) (решение ОДУ), где x – имя переменной, относительно которой решается уравнение, xk – конец интервала интегрирования (начало интервала интегрирования указано ранее, в начальных условиях)

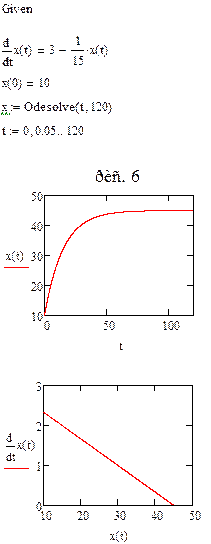
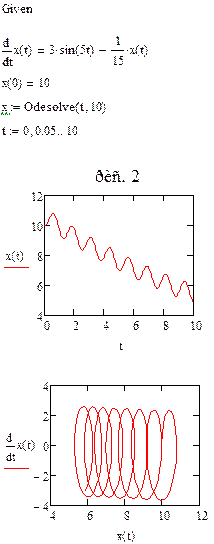
Вывод: исследовалось виляние параметров дифференциальных уравнений первого порядка с постоянными коэффициентами на решение

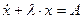
Данная система моделировалась в Mathcad при значении

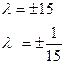
По результатам компьютерного моделирования получаем, что:

• при решение x(t) устойчиво (рисунок 2, 3, 6, 7)

что объясняется наличием в решении слагаемого 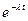- убывающей экспоненты

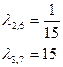
• при решение x(t) неустойчиво (рисунок 1, 4, 5, 8)

что объясняется наличием в решении слагаемого 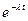- возрастающей экспоненты

)

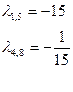Дата добавления: 2015-04-24