Основы статистических испытаний сетевой модели

ОЦЕНКА НАДЕЖНОСТИ СЕТЕВОЙ МОДЕЛИ МЕТОДОМ СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ

Задание для самостоятельного выполнения работы

Студенты дневной и заочной форм обучения выполняют данную работу по одному из вариантов, приведенных в табл. 5. Выбор варианта задания производится студентом самостоятельно следующим образом: номер варианта принимается по последней цифре шифра, указанного в зачетной книжке студента, если первая буква фамилии студента находится в промежутке алфавита от «А» до «И» включительно, то из первого десятка вариантов (от 1 до 10); если первая буква фамилии находится в интервале «К» – «Т», то – по второму десятку номеров (от 11 до 20); если фамилия студента начинается с буквы из интервала «У» – «Я», то – по третьему десятку номеров (от 21 до 30).

По данным выбранного варианта задания (табл. 5) студент должен:

1) построить сетевую модель, используя временные оценки Т_нв как детерминированные;

2) произвести расчет детерминированных параметров сетевой модели графическим и табличным способами;

3) самостоятельно приняв вероятностные временные оценки Т_о и Т_п по каждой работе, произвести необходимые расчеты и оценить надежность сетевой модели.

Таблица 5

Варианты индивидуальных заданий к работе
«Оценка надежности сетевой модели производства работ»

Вариант	Код работ	Тнв, дн.	Вариант	Код работ	Тнв, дн.
	1-2 1-3 1-4 2-5 3-5 3-6 3-8 4-6 4-7 5-7 6-7 7-8			1-2 2-3 2-4 3-5 3-9 4-5 4-7 5-6 6-8 6-9 7-6 7-10 8-10 9-10
	1-2 1-3 2-6 3-4 3-5 4-6 5-6 5-7 6-8 7-8			1-2 1-5 2-3 2-4 3-4 3-5 3-7 4-6 5-8 6-7 6-9 7-9 8-9

Продолжение табл. 5

Вариант	Код работ	Тнв, дн.	Вариант	Код работ	Тнв, дн.
	1-2 2-3 2-4 3-5 3-7 4-5 4-8 5-6 6-7 6-8 7-9 8-9 9-10			1-2 1-6 2-3 2-4 3-5 3-9 4-6 4-8 5-7 6-11 7-9 7-10 7-12 8-9 8-11 9-11 10-12 11-12
	1-2 1-5 2-3 2-4 3-4 3-5 4-6 5-6 6-7			1-2 1-3 2-3 2-4 3-4 3-5 4-5 4-6 5-6
	1-2 1-6 1-10 2-3 2-4 2-5 3-6 4-6 4-7 5-7 6-8 7-8 8-9 8-10 10-11 11-12			1-2 1-3 1-4 1-5 1-6 2-4 2-7 3-5 3-10 4-8 5-7 6-9 7-10 8-10 9-10 10-11

Продолжение табл. 5

Вариант	Код работ	Тнв, дн.	Вариант	Код работ	Тнв, дн.
	1-2 2-3 2-4 3-5 3-7 4-5 4-8 5-6 6-7 6-9 7-11 8-9 8-12 9-10 10-11 10-12 11-13 12-13 12-14 13-14			1-2 1-3 1-4 1-5 1-6 2-7 3-8 4-8 5-11 6-10 7-14 8-9 9-11 9-12 10-11 10-14 11-13 12-13 12-14 13-14
	1-2 1-3 1-4 2-5 2-6 3-4 3-5 3-7 4-5 5-6 5-7 5-8 6-8 6-9 7-8 8-9			1-2 1-3 1-4 2-5 2-6 3-7 4-9 5-11 6-7 6-8 7-8 7-9 8-11 9-10 9-11 10-11
	1-2 1-3 1-4 1-5 1-7 2-3 2-5 3-6 4-5 4-7			1-2 1-5 2-3 2-4 2-8 3-4 3-5 3-7 4-6 5-9

Продолжение табл. 5

Вариант	Код работ	Тнв, дн.	Вариант	Код работ	Тнв, дн.
	4-9 5-6 5-10 6-7 6-9 7-8 7-9 8-9 8-10 9-10			6-8 7-10 8-13 9-12 10-11 11-12 11-14 12-15 13-15 14-15
	1-2 2-3 2-4 2-5 3-6 4-6 5-7 5-9 6-8 7-8 8-9			1-2 2-3 2-4 2-5 3-5 4-5 4-6 4-7 5-7 6-7 7-8
	1-2 1-3 2-4 2-5 3-4 3-9 4-6 5-6 5-8 6-7 7-8 7-9 8-10 9-10			1-2 1-3 1-4 2-3 2-4 3-5 4-6 4-7 5-7 5-9 6-8 7-9 7-10 8-10 9-10
	1-2 1-3 1-4 2-3 2-7 3-5 4-5 4-8 5-6 6-7			1-2 1-3 2-3 3-4 3-5 3-7 3-12 4-6 5-7 6-8

Продолжение табл. 5

Вариант	Код работ	Тнв, дн.	Вариант	Код работ	Тнв, дн.
	6-8 6-9 7-9 8-9			7-8 8-9 8-10 8-11 9-10 10-11 11-12
	1-2 1-3 2-4 2-5 3-4 3-9 4-6 5-6 5-8 6-7 7-8 7-9 8-10 9-10			1-2 1-3 1-4 2-5 3-6 4-7 5-6 5-8 6-8 6-9 7-9 8-10 8-11 9-11 10-11
	1-2 1-3 1-4 2-3 2-7 3-5 4-5 4-8 5-6 6-7 6-8 6-9 7-9 8-9			1-2 2-3 3-4 3-6 4-5 5-6 5-9 6-7 6-9 6-11 7-8 8-9 9-10 10-11 11-12
	1-2 1-3 1-4 2-6 3-5 3-6 4-5 4-7 5-6			1-2 1-3 1-4 2-3 2-4 2-5 2-6 2-7 3-5

Окончание табл. 5

Вариант	Код работ	Тнв, дн.	Вариант	Код работ	Тнв, дн.
	5-7 6-8 6-9 7-8 7-9 8-10 9-10			3-6 4-5 4-7 5-6 5-7 5-8 6-8 7-8
	1-2 1-3 1-4 2-4 2-5 3-4 3-6 4-5 4-6 4-7 5-7 5-8 6-7 6-8 7-8			1-2 1-3 1-4 2-6 3-4 3-5 3-7 4-5 4-6 5-6 5-7 6-8 6-9 7-8 7-9 8-10 9-10

Контрольные вопросы

1. Сформулируйте определение сетевой модели строительного производства. Какова типология сетевых моделей?

2. Что такое "путь" в сетевой модели? Дайте определение критического пути.

3. Назовите основные параметры сетевой модели и дайте их определение.

4. Дайте сравнительную характеристику детерминированных и вероятностных сетевых моделей.

5. Сформулируйте определение надежности сетевой модели. Как производится количественная оценка надежности сетевой модели?

Рассмотренный в предыдущем разделе метод оценки надежности сетевых графиков основан на анализе критических путей. Если критический путь (пути) в ходе реализации графика не меняются, то метод считается точным. В случаях, когда критический путь может измениться, метод чаще всего дает ошибочные результаты [7]. В этом случае целесообразно оценивать надежность графиков с помощью статистического проигрыша (статистических испытаний).

Метод статистических испытаний (метод Монте-Карло) представляет собой совокупность приемов и правил, позволяющих имитировать (воспроизводить) вероятностные процессы с применением при этом аппарата случайных чисел. Этот метод в настоящее время является наиболее универсальным из численных методов решения математических, инженерных, экономических и любых других задач, имеющих и вероятностный и детерминированный характер [16].

Метод основан на многократном проигрывании процессов на построенной модели с целью получения как можно большего числа значений количественных характеристик. Затем полученные значения подвергаются статистической обработке, что позволяет выявить соответствующие закономерности данного процесса в виде ряда количественных оценок. Например, многократно изменяя длительности работ сетевой модели, можно в итоге получить выборку значений длительности критического пути, на основании которой оценить вероятность выполнения проекта в заданные сроки.

Решение задач методом Монте-Карло включает следующие этапы:

1) разработку и построение структурной схемы процесса (например, сетевого графика); выявление основных звеньев и связей;

2) формальное описание процесса (алгоритм расчета критического пути);

3) собственно моделирование – воспроизведение процесса в соответствии с разработанной структурной схемой и формальным описанием;

4) накопление результатов моделирования, их статистическую обработку, анализ и обобщение.

Для моделирования процесса используются так называемые случайные числа с различными законами распределения. Чаще всего случайные числа – это равномерная случайная последовательность чисел в интервале 0–1. Такие последовательности случайных чисел можно получить тремя способами:

– построением таблиц случайных чисел;

– созданием генераторов случайных чисел;

– использованием метода псевдослучайных чисел.

В данном пособии используется таблица нормальных нормированных случайных отклонений [7]. С их помощью многократно изменяются продолжительности работ t_ij сетевой модели:

t_ij = Т_ож + (13)

где Т_ож – расчетная продолжительность работ вероятностной сетевой модели; = 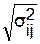– среднеквадратическое отклонение от Т_ож; 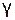– нормированные случайные отклонения в долях (прил. 2).

Изменив продолжительности работ сетевой модели, производим ее расчет с целью определения длины критического пути Т_кр. Такой однократный расчет при статистических испытаниях принято называть реализацией модели. Проведя N реализаций сетевой модели, получим в итоге N значений продолжительности критического пути. При этом часть значений Т_кр будет удовлетворять условию:

Т_кр Т _д, (14)

где Т _д – директивный (заданный) срок выполнения комплекса работ.

Вероятность выполнения этого условия

р(Т_кр Т _д) = , (15)

где N₁ – число реализаций, в которых выполняется условие (14); N – общее число реализаций.

При достаточно большом числе N на основе статистической обработки значений t_ij, , T_kp и других показателей можно с определенной степенью достоверности установить законы распределения случайных величин и осуществить имитационное моделирование производственного процесса [16].

Дата добавления: 2015-04-24