Понятие о корреляционной зависимости

Корреляционная связь - это согласованные изменения двух при­знаков или большего количества признаков (множественная корреляци­онная связь). Корреляционная связь отражает тот факт, что изменчи­вость одного признака находится в некотором соответствии с изменчи­востью другого.

Корреляционная зависимость - это изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака.

Оба термина – корреляционная связь и корреляционная зависи­мость – часто используются как синонимы. Между тем, согласованные изменения признаков и отражающая это корреляционная связь между ними может свидетельствовать не о зави­симости этих признаков между собой, а зависимости обоих этих при­знаков от какого-то третьего признака или сочетания признаков, не рассматриваемых в исследовании.

Зависимость подразумевает влияние, связь – любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной связи, они свидетельствуют лишь о том, что изменениям одного при­знака, как правило, сопутствуют определенные изменения другого, но находится ли причина изменений в одном из признаков или она оказы­вается за пределами исследуемой пары признаков, нам неизвестно.

Корреляционные связи различаются по форме, направлению и силе.

По форме корреляционная связь может быть прямолинейной или криволинейной. Прямолинейной может быть, например, связь между количеством тренировок на тренажере и количеством правильно решае­мых задач в контрольной сессии. Криволинейной может быть, напри­мер, связь между уровнем мотивации и эффективностью выполнения задачи. При повышении мотивации эффективность вы­полнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации, которому соответствует максимальная эффектив­ность выполнения задачи; дальнейшему повышению мотивации сопутст­вует уже снижение эффективности

По направлению корреляционная связь может быть положитель­ной (" прямой "), если коэффициент корреляции положительный и отрицательной (" обратной "), если коэффициент корреляции отрицательный.

При положительной прямолинейной корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значе­ниям одного признака - низкие значения другого. При отрицательной корреляции соотношения обратные.

Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции.

Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции. Максимальное воз­можное абсолютное значение коэффициента корреляции r = 1,00; мини­мальное r=0.

Будем использовать общую классификацию корреляционных связей:

1) сильная, или тесная при коэффициенте корреляции r >0,70;

2) средняя при 0,50< r <0,69;

3) умеренная при 0,30< r <0,49;

4) слабая при 0,20< r <0,29;

5) очень слабая при r <0,19.

Следовательно, чтобы охарактеризовать связь необходимо вычислить коэффициент корреляции. В общем виде формула для подсчета коэффициента корреляции такова: 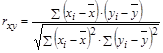, где х_i - значения, принимаемые в выборке X, y_i — значения, принимаемые в выборке Y; 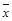— средняя по X, 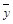— средняя по Y.

Метод ранговой корреляции Спирмена позволяет определить тес­ноту (силу) и направление корреляционной связи между двумя призна­ками или двумя профилями (иерархиями)признаков. Для подсчета ранговой корреляции необходимо располагать двумя рядами значений, которые могут быть проранжированы. С этим методом предлагается ознакомиться самостоятельно.

Дата добавления: 2015-04-24