Основы булевой алгебры

Простейшие логические функциидвух переменных.

Для описания функционирования логических элементов разработана специальная алгебра, называемая по имени её создателя Джона Буля, булевой алгеброй. В булевой алгебре производятся операции над переменными, принимающими два значения – 0 и 1. Из всего множества логических функций (для n переменных число функций равно 2²ⁿ ) на практике используется всего около 10

Некоторые из них приведены в таблице.

Таблица 4.1 – Логические функциидвух переменных

Функционально полные системы логических элементов

Минимальный набор элементарных функций, позволяющий реализовать любую сколь угодную функцию, составляет функционально полную систему. Такая система может состоять из одной (например ИЛИ-НЕ или И-НЕ) или двух (НЕ и ИЛИ или НЕ и И). Выбор той или иной системы зависит от наличия элементной базы.

Таблица 4.2 – Правило преобразования логических выражений

Правило преобразования	Логическое выражение
Правило деМоргана:
для ИЛИ (дизъюнкции)
для И (конъюнкции)
для И - НЕ (функции Шеффера)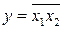
для ИЛИ – НЕ (функции Пирса)
Соотношение для ИЛИ
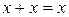
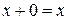
Соотношение для И

Все эти соотношения можно легко получить непосредственно проверкой. Провести несколько примеров при заполнении таблицы.

Таблица 4.3 – Законы и логические соотношения алгебры логики

Законы алгебры логики	Соотношения
Закон коммутативности (переместительный) для дизъюнкции ИЛИ для конъюнкции И для функции Шеффера И–НЕ для функции Пирса ИЛИ–НЕ для суммы по модулю 2
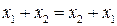
Закон ассоциативности (сочетательный) для ИЛИ И исключающее ИЛИ
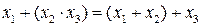
Закон дистрибутивности (распределительный) для ИЛИ И исключающее ИЛИ

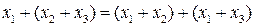
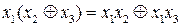
Закон ассоциативности не применим для И–НЕ и ИЛИ–НЕ.

Таким образом, по отношению к основным логическим функциям ИЛИ и И справедливы законы обычной алгебры – операции логического сложения предшествует операция логического умножения, можно заключить выражение в скобки и раскрывать их, выносить общий множитель за скобку.

Представление логических функций

Логические функции могут быть представлены как в табличной, так и в аналитической форме. Табличная форма - см. таблица 1.

Рассмотрим аналитический способ. Пусть задана логическая функция.

В любое из произведений логическая переменная входит только один раз в прямом или инверсном виде. Каждое такое произведение называется минтермом и обозначается через m_i. Для n переменных число минтермов 2ⁿ.

Это же уравнение можно представить:

Каждая такая сумма называется макстермом и обозначается M_i. Полное число макстермов равно .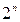

Можно показать, что сумма минтермов равна единице: 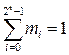, а произведение макстермов равно нулю: 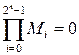. Также и для .

Дизъюнктивная и конъюнктивная нормальные формы

Любую логическую функцию можно представить в виде суммы минтермов или произведения макстермов. Существует две формы записи логических функций – в виде суммы элементарных конъюнкций–минтермов–дизъюнктивная нормальная форма ДНФ или в виде произведения элементарных дизъюнкций–макстермов–нормальная конъюнктивная форма КНФ.

Совершенной ДНФ (СДНФ) и СКНФ называют соответственно ДНФ, содержащую все минтермы, а КНФ – содержащую все макстермы.

Для перехода от нормальной формы к совершенной для получения СКНФ необходимо домножить все простые сомножители на выражение , которое всегда тождественно равно 1, или сумму для получения СДНФ с , которое тождественно равно 0. Этим способом пользуются, если число аргументов не превышает 4.

При 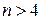пользуются картами минтермов Карно (Вейча), представляющих собой таблицы (прямоугольные) с клетками, число которых равно удвоенному количеству переменных – для прямых и инверсных значений. Каждая единица, помещенная в клетку карты Карно, соответствует своему минтерму. Чтобы нанести на карту выражение a b надо поставить 1 во всех клетках относящихся к a и b одновременно. Если в клетке появляется две или более 1, считается, что там 1 единица.

Рисунок 4.1 – Карта минтермов

Упрощение булевых функций

1. Целесообразность упрощения.

Рассмотрим выражение:

Этот метод преобразования называется методом Квайна.

Преобразованная функция намного проще исходной. При построении аппаратуры стремятся к реализации структурных схем, обеспечивающих максимальный расход оборудования.

Построение комбинационных логических схем по заданным булевым выражениям

Как правило, построение и расчет любой схемы осуществляется начиная с ее выхода. Допустим задано булево выражение: F =`B A + B`A + C`B. Первый этап: выполняется логическое сложение, логическую операция ИЛИ, считая входными переменными функции `B A, B`A и C`B: Второй этап: к входам элемента ИЛИ подключаются логические элементы И, входными переменными которых являются уже A, B, C и их инверсии: Третий этап: для получения инверсий `A и`B на соответствующих входах ставят инверторы: 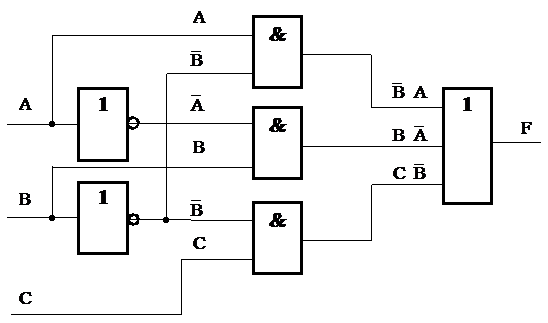Данное построение основано на следующей особенности, – поскольку значениями логических функций могут быть только нули и единицы, то любые логические функции могут быть представлены как аргументы других более сложных функций. Таким образом, построение комбинационной логической схемы осуществляется с выхода ко входу.

2. Задачи минимизации.

Под минимизацией булевой функции чаще всего понимают нахождение простого её представления в виде суперпозиции операций, представляющих какую либо фиксированную, функционально полную систему.

Наиболее простым считается представление, содержащее минимальное число суперпозиций.

Каноническая задача минимизации – представление заданной булевой функции в ДНФ, содержащее минимальное число букв.

3. Методы упрощения.

Карта Карно отличается от карты Вейча порядком расположения символов.

Карты Карно оказываются более удобными при анализе и синтезе последовательных схем (например, счетчиков или регистров).

Рисунок 4.2 – Карта Вейча

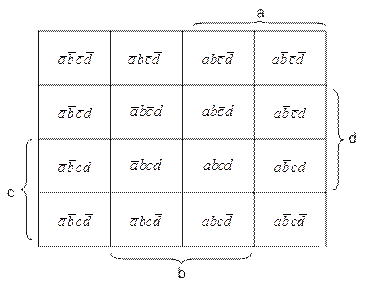
Рисунок 4.3 – Карта Карно

Рисунок 4.4 – Нанесение на карту Вейча выражений

После нанесения выражения на карту, его можно прочитать.

Этот рисунок соответствует:

Упрощение достигается склеиванием единиц на карте Вейча. Склеивать можно квадраты, двойные квадраты, полные столбцы, а также два соседних минтерма и минтермы находящиеся в противоположных концах столба или строки.

Минимальные формы булевой функции получают тогда, когда склеивается наибольшее количество минтермов, а булеву сумму, получаемую после упрощения.

Дата добавления: 2015-03-29