Рост массы растений

Задача. Необходимо найти уравнение роста целого растения, которое описывает изменение сухой массы растения в течение всего вегетационного периода. Параметры уравнения должны иметь физиологический смысл.

Гипотезы

1. Растение как объект моделирования определяется только одним параметром – своей сухой массой (M). М является зависимой переменной, варьирующей во времени t, где t – независимая переменная.

2. Рост происходит при увеличении количества одного субстрата S.

3. Скорость ростовой реакции прямо пропорциональна уровню субстрата S и сухой массе растения М, так что рост является автокаталитическим процессом. Скорость ростовой реакции равна kMS, где k – константа.

Математическая модель.

Из третьей гипотезы следует, что:

dM/dt = kSM [1]

Это дифференциальное уравнение не может быть решено, так как уровень субстрата S в процессе роста изменяется. Если S и M измерять в одинаковых единицах при предположении, то не происходит потеря вещества при превращении S в М, то:

dM = – dS [2]

Отсюда следует, что увеличение сухой массы точно соответствует уменьшению субстрата. Это уравнение можно записать в виде d (M + S) = 0, которое при интегрировании дает:

M + S = M_i + S_i = const [3]

где M_i и S_i – значения M и S в момент времени t = 0. M и S не могут быть отрицательными, поскольку теряют всякий физиологический смысл. М достигает максимального и конечного значения, когда исчерпывается субстрат S = 0. Соответственно, уравнение 3 можно записать в виде:

M + S = M_f = M_i + S_i [4],

где M_f – максимальное значение M. Заменяя S из уравнения 4 в уравнении 1, получим:

dM / dt = k (M_f – M) M [5]

Это уравнение представляет модель в дифференциальной форме. Система имеет только одно переменное состояние, поэтому достаточно лишь одного уравнения.

Уравнение 5 принадлежит к типу уравнений с разделяемыми переменными, и его можно представить в виде:

=

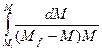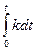
Левую часть преобразуем следующим образом:

=

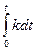
Интегрирование дает:

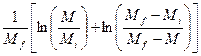= kt

из которого получаем:

M = 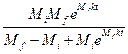[6]

Рис. 1 Кривая роста целого растения, построенная на основе уравнения 6 при Mi = 1, Mf = 10 и k = 0,1. Обозначения: М – масса, t – время.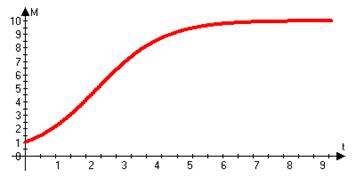

Константы полученного уравнения имеют приближенный физиологический смысл:

М_i – начальное значение сухой массы растения;

M_fk – максимальная удельная скорость роста, достигаемая растением в начальной фазе роста, когда отсутствует ограничение субстратом;

M_f – конечная масса растения, которая определяется начальным количеством доступного субстрата и начальной массой сухого вещества растения.

График, отражающий рост растения согласно полученному уравнению, представлен на рис. 1.

Дата добавления: 2015-04-24