Методика измерений

а) Определение степени поляризации частично поляризованного света

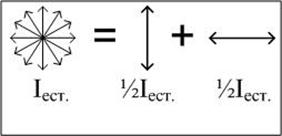Пусть на неидеальный поляроид падает естественный свет интенсивностью I_ест. Представим его в виде суперпозиции двух некогерентных линейно поляризованных во взаимно перпендикулярных плоскостях лучей одинаковой интенсивности (рис.3.9). Предположим, что через неидеальный поляроид без поглощения проходит луч, поляризованный в направлении оптической оси, (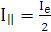), а луч, поляризованный перпендикулярно оптической оси, частично поглощается, так что 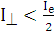. Пусть

. (3.8)

Величина K характеризует качество неидеального поляроида. Для идеального . Если в качестве анализатора использовать идеальный поляроид, то обе величины, и , можно измерить, пропустив частично поляризованный свет, вышедший из неидеального поляроида, через идеальный поляроид и измерив интенсивности I_max и I_min; это будут I_॥ и I_^ соответственно. Тогда

. (3.9)

Связь между качеством неидеального поляроида и степенью поляризации Р света, прошедшего через такой поляроид, можно установить из определения (3.10) степени поляризации

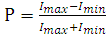: (3.10)

, (3.11)

откуда

. (3.12)

Пусть естественный свет проходит через два одинаковых неидеальных поляроида. При параллельной ориентации их оптических осей составляющая естественного света, параллельная оптической оси обоих поляроидов, пройдёт без изменения:

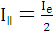, (3.13)

а перпендикулярная будет ослаблена в 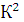раз:

. (3.14)

Полная интенсивность света, измеренная прибором, поставленным после прохождения светом двух неидеальных одинаковых поляроидов, равна их сумме (эти две составляющие некогерентны):

. (3.15)

При перпендикулярной ориентации оптических осей двух одинаковых поляроидов составляющая естественного света, параллельная оптической оси первого поляроида, проходит через первый без изменения, и ослабляется вторым в К раз:

, (3.16)

а перпендикулярная будет ослаблена только первым тоже в раз:

. (3.17)

Полная интенсивность света равна их сумме:

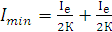. (3.18)

Отношение интенсивностей при параллельной и перпендикулярной ориентации оптических осей:

. (3.19)

Величина n измеряется экспериментально. Уравнение (3.21) можно решить относительно K:

;

;

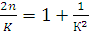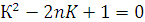. (3.20)

По определению K>1, тогда знак минус в (3.22) надо исключить. Итак,

. (3.21)

Затем можно рассчитать степень поляризации света, прошедшего через один поляроид:

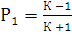, (3.22)

и через два параллельных поляроида:

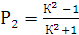. (3.23)

Очевидно, закон Малюса для неидеальных одинаковых поляроидов примет вид (3.24)

. (3.24)

При 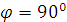(поляроиды скрещены) из (3.26) получим: , а при 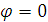(поляроиды параллельны) .

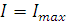б) Интерференция поляризованных лучей. Определение степени анизотропии

При нормальном падении пучка лучей на пластинку из кристалла, оптическая ось y которого параллельна преломляющей поверхности, обыкновенный и необыкновенный лучи идут по одному направлению, но с разными скоростями. Пусть на такую пластинку падает плоско поляризованный луч с амплитудой электрического вектора E ₀, плоскость поляризации которого составляет с плоскостью главного сечения пластинки ОО´ угол φ. Тогда в пластинке возникнут оба луча, обыкновенный (о) и необыкновенный (е) (рис. 3.10), и они будут когерентны. В момент их возникновения в пластинке разность фаз между ними равна нулю, но она будет возрастать по мере проникновения лучей в пластинку. Подсчитаем эту разность фаз.

Оптическая разность хода Δ равна разности оптических длин путей обыкновенного и необыкновенного лучей:

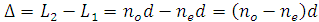. (3.25)

Отсюда разность фаз между обоими лучами равна

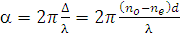, (3.26)

где 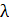– длина волны в вакууме.

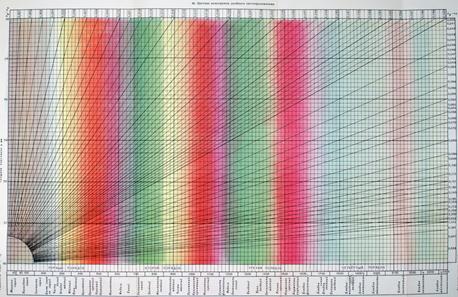
Пусть на анизотропную пластинку падает линейно поляризованный белый свет. Длины волн белого света имеют всевозможные значения в интервале приблизительно 380÷780 нм. Получающаяся в кристалле разность хода для лучей одних длин волн будет равна четному, для других – нечетному числу полуволн. Поэтому волны одних длин будут при интерференции уничтожаться, другие, наоборот, усиливаться. В результате отношение интенсивностей различных цветов будет иным, чем в белом свете, и кристалл будет казаться окрашенным. Каждой разности хода соответствует некоторая интерференционная окраска. Интерференционные окраски не являются чистыми монохроматическими спектральными цветами, но представляют собой смесь в различных пропорциях всех цветов, входящих в состав белого, кроме тех, которые уничтожаются при данной разности хода. Наблюдение и исследование интерференционных цветов имеет очень большое значение в кристаллооптической методике.

Познакомиться с цветами, получающимися при различных разностях хода. В таблице Мишеля-Леви (рис.3.11) последовательно отображаются переходы интерференционных цветов, наблюдаемые при изменении толщины образца.

	Рис.3.11

Дата добавления: 2015-03-29