
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тень от абаки на колонну
|
|
|
|
На рис. 50 изображена абака, имеющая форму шестигранной плиты, отбрасывающая тень на полуцилиндрическую колонну.
Вначале определим контур собственной тени на шестигранной плите. Проанализируем освещенность ее граней. При заданном направлении S светового потоканеосвещенными окажутся правая, нижняя и задняя грани плиты (они будут находиться в собственной тени). Поскольку правая грань видна на фронтальной проекции – выделим ее бледным тоном. Определим контур собственной тени полушестигранника. Ввиду того, что последний примыкает к стене, можно отметить e' = eТ' , f' = fТ', и отрезок [ EF ] входит в состав контура собственной тени, т.к. стена освещена, а задняя грань в тени. Следующим отрезком контура будет [ EL ], потому что верхняя грань освещена, а правая в тени. Рассуждая аналогично, определяем другие отрезки, входящие в этот контур – это [ LA ], [ AB ], [ BQ ] и [ QF ]. Определение замкнутого контура плиты завершено.
На этом же рисунке показана падающая тень плиты на стену независимо от полуколонны (ее контур, находящийся за непрозрачной колонной, изображен точечными линиями). Заметим, что часть цилиндрической колонны находится в собственной тени (ее построение рассмотрено в предыдущем разделе), которая на чертеже выделена бледным тоном.
Тени ребер [ EL ] и [ LA ] по построению полностью оказались на стене, а ребро [ AB ] частично отбрасывает тень на стену в виде прямой, параллельной ребру, а также на колонну. Лучевая плоскость, проходит через отрезок [ AB ], перпендикулярный плоскости W, поэтому на основании признака перпендикулярности прямой и плоскости, она является профильно-проецирующей (рис. 51).
На поверхности цилиндра от пересечения с ней образуется эллипс, поскольку плоскость пересекает все его образующие. Кроме того, она равно наклонена к плоскостям проекций H и V, поэтому проекциями этого эллипса будут окружности (или дуги окружностей, т. к. величина ребра конечна). Горизонтальная проекция окружности совпадает со следом цилиндра на плоскости H. Для нахождения фронтальной проекции окружности определим точку bТ' и проведем через нее дугу, радиус которой равен радиусу цилиндра, а ее центр лежит на оси.
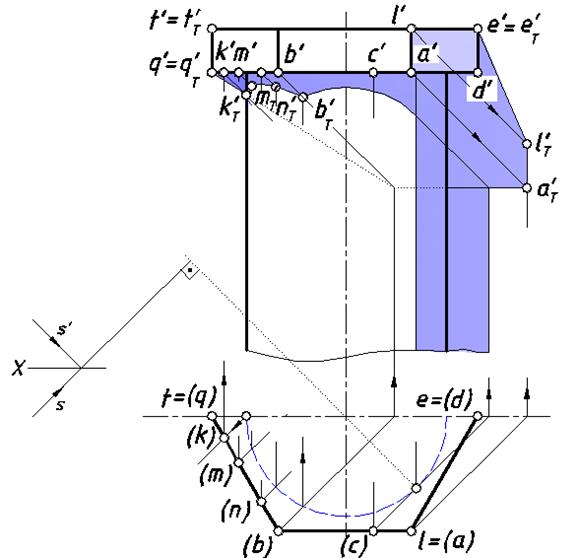
Рис. 50. Собственные и падающие тени абаки на колонну
Отрезок [ BQ ] также отбрасывает тень на поверхность цилиндра. Через него проходит лучевая плоскость общего положения, которая, пересекая цилиндр, оставляет на нем тень виде дуги эллипса.
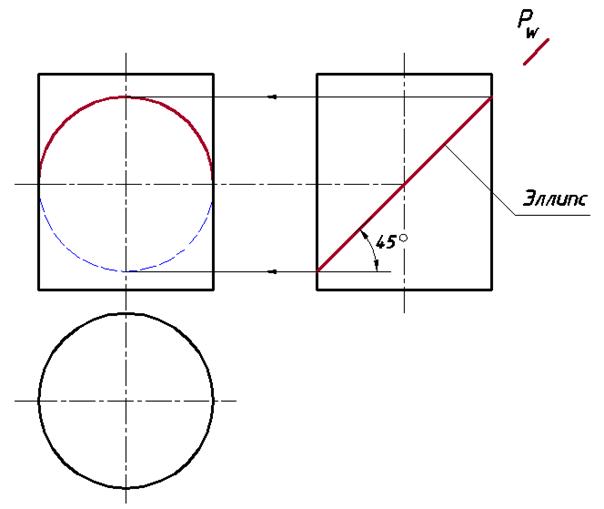
Рис. 51. Сечение цилиндра профильно-проецирующей плоскостью
Построение этого эллипса выполняем по множеству точек. На отрезке [ BQ ] берем случайные точки (на рис. 50 это точки M (m, m ')
и N (n, n ')). Строим точки пересечения лучей, проходящих через эти точки, с поверхностью цилиндра (падающие тени точек) и соединяем их плавной кривой. С помощью обратного луча определяем точку K (k, k ') на отрезке [ BQ ], которая отбрасывает тень на левую очерковую образующую цилиндра.
Построение падающей тени цилиндра рассматривалось ранее.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1824; Нарушение авторских прав?; Мы поможем в написании вашей работы!